Heap

A Heap is a complete binary tree in which every node satisfies the heap property -

1. Complete binary tree
2. The root will always be minimum from the rest of the nodes (for min heap and vice versa for max heap)

Note: When we say heap, it means a Binary heap. Other kinds of heaps exist like Binomial heaps and Fibonacci heaps, but those are out of the scope of our discussion.

Heaps are also used for implementing priority queues.

Complete Binary Tree

First of all, let's understand what is a complete binary tree.

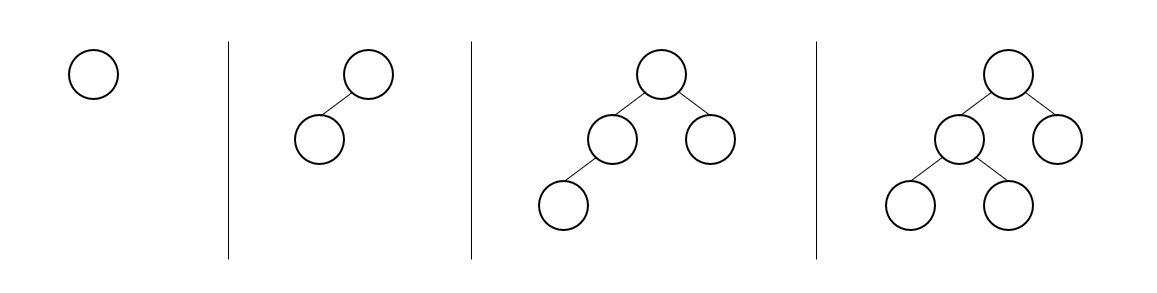
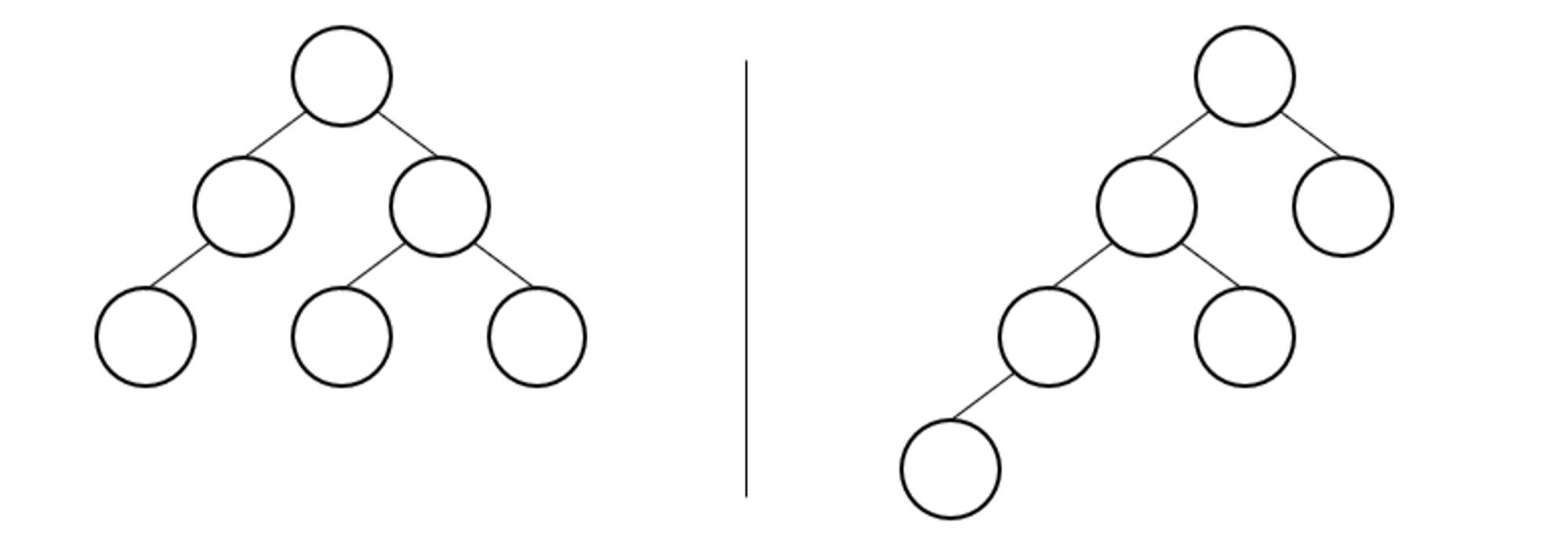
It is a binary tree but to be qualified as a complete binary tree every level needs to be filled (the last level is the exception, in case there are not a sufficient number of nodes)

In other words, we can say fill the nodes from top to bottom and from left to right in the form of a binary tree to get a complete binary tree.

To understand various types of trees and binary trees refer to these articles-

• Introduction to Trees
• Introduction to Binary Trees

Example of Complete binary trees -

These are not complete binary trees -

Height of Complete binary tree

In the worst case, the height of the complete binary tree will be O(log n) because the height is always balanced.

Store Complete binary tree in memory

Now we have the idea that to maintain heap data structure we can use a complete binary tree but the next question is how to store it in memory.

Earlier we discussed about storing it into a Binary search tree pattern to get the height of O(log n) but with this approach for any new insertion, it will take O(n). We can do better than this.

To optimise further, we can store the data in the form of an array and visualise it as a tree.

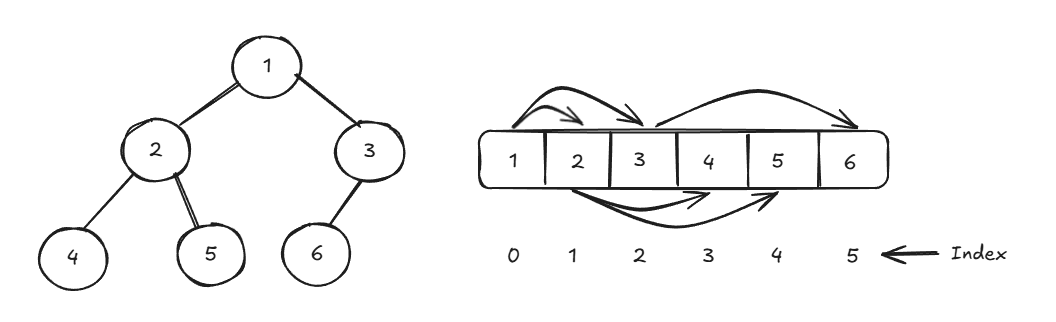
We can represent the level order of a tree like this in form of an array.

Parent-child relationship in complete binary tree

Now we can store the heap data in the form of an array and visualise it as a tree. But in the case of the Binary search tree, we can easily the left and right children. Since our goal is to visualise it as a tree so let's understand how to establish parent child relationship in such case.

For elements at the ith position,

• its left child will be at the 2i+1 position
• and the right child will be at the 2i+2 position

For example -

• 1 is at the index 0

  • its left child is at 2*0+1=1 position
  • and the right child is at 2*0+2=2 position

• 2 is at the index 1

  • its left child is at 2*1+1=3 position
  • and the right child is at 2*1+2=4 position

• 3 is at index 2

  • its left child is at 2*2+1=5 position
  • and the right child is at 2*2+2=6 position. Since 6 is more than the length of the array this means there is no right child of 3

Similarly to get the parent of any element, we can use

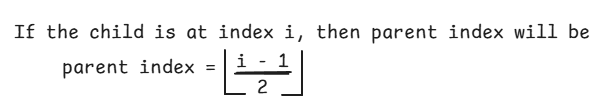
For example

• 4 is at index 3 and its parent is at of (3-1)/2 = 1
• 5 is at index 4 and parent is at (4-1)/2 = 1.5 take the floor value of 1.5 i.e., 1

Heap order property

Heaps have the following two properties -

1. Complete binary tree
2. Heap order property
   1. Min-heap - 0 index element will be the minimum and the value of each node will be lesser than the left and right child. Lower the value higher the priority
   2. Max-heap - 0 index element will be the maximum and the value of each node will be higher than the left and right child. Higher the value higher the priority

Min-heaps are commonly used to implement priority queues. For the heapsort algorithm, we use max-heaps.