Priority Queue

This article dives into the fundamentals of Priority Queues exploring their key operations, use cases, and detailed implementations in Python, Java, C++, Go, and Rust, with a focus on efficiency and real-world applications.

Priority Queue

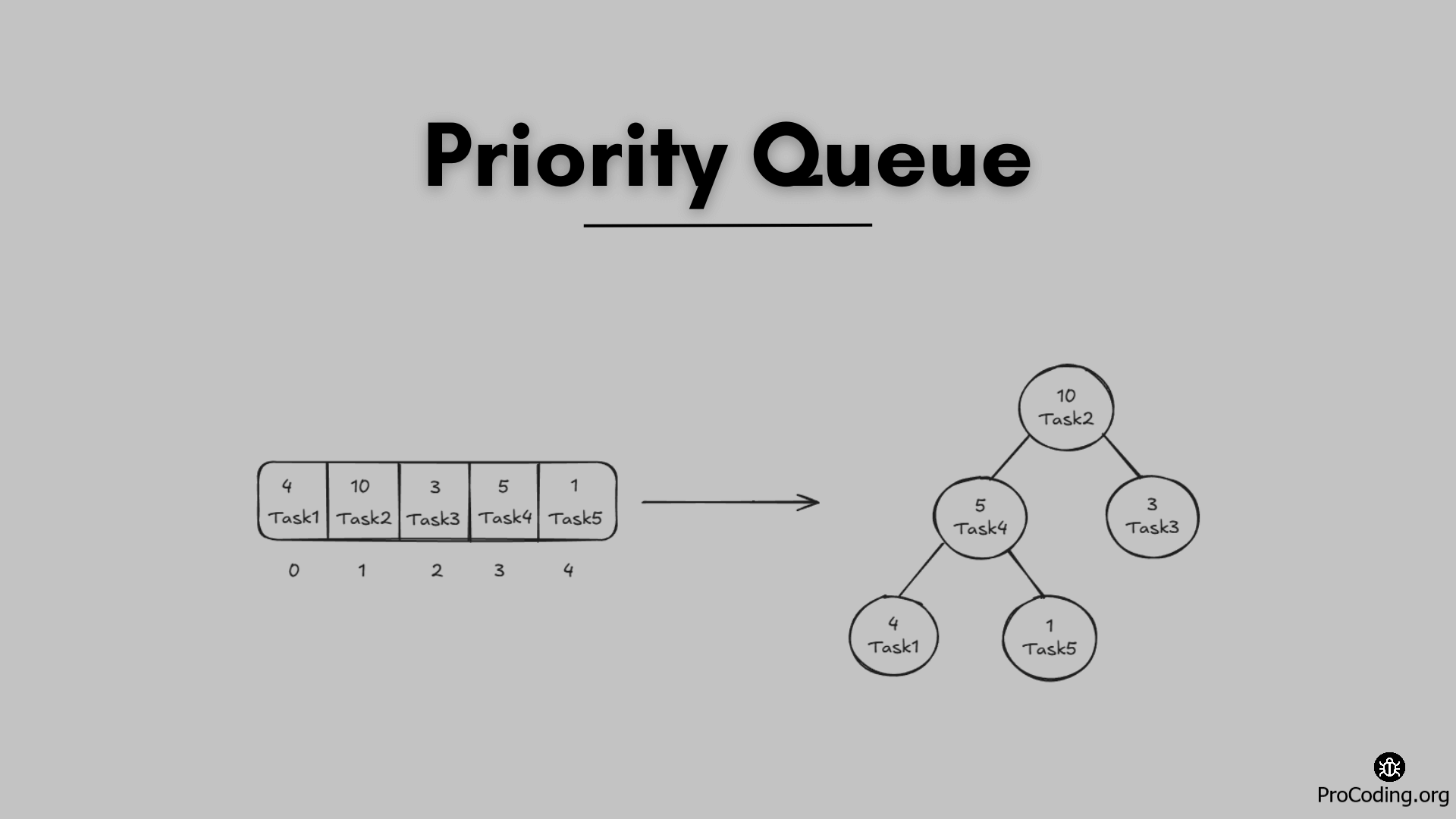
A priority queue is a specialized type of data structure where each element is associated with a priority, and the element with the highest priority is served before other elements. Unlike regular queues, where elements are served in a first-come, first-served (FIFO) manner, priority queues order elements based on their priority.

Key Concepts of Priority Queues

Priority: Each element in a priority queue has a priority level. Elements with higher priorities are dequeued before elements with lower priorities.
Order of Insertion: When two elements have the same priority, the order of insertion is maintained. The element that was inserted first will be dequeued first (this is called a stable priority queue).
Underlying Data Structure: Priority queues can be implemented using different data structures, but heaps (particularly binary heaps) are the most common due to their efficient insertion and deletion operations.

Types of Priority Queues

Min-Priority Queue: In a min-priority queue, the element with the lowest priority is dequeued first. This is often implemented using a min-heap.
Max-Priority Queue: In a max-priority queue, the element with the highest priority is dequeued first. This can be implemented using a max-heap or by negating the priorities in a min-heap.

Operations on a Priority Queue

Insertion (enqueue): Adding a new element to the priority queue. The element is placed in the correct position based on its priority.
Deletion (dequeue): Removing the element with the highest (or lowest in a min-priority queue) priority from the queue.
Peek: Viewing the element with the highest priority without removing it from the queue.
Is Empty: Checking if the priority queue is empty.
Size: Returning the number of elements currently in the priority queue.

Which data structure to use for Priority Queue?

To implement a priority queue, several data structures can be used, each with its own trade-offs in terms of time complexity and ease of implementation. The most common data structures for implementing a priority queue are:

1. Binary Heap

Type: Binary Tree
Variants: Min-Heap, Max-Heap
Time Complexity:
- Insertion: O(log n)
- Deletion (Extract-Min/Extract-Max): O(log n)
- Peek (Get-Min/Get-Max): O(1)
Pros:
- Efficient for implementing a priority queue due to logarithmic time complexity for insertion and deletion operations.
- Heaps are relatively simple to implement.
Cons:
- Not ideal for dynamic or highly variable data where you need to frequently change priorities (e.g., decrease-key operations).

2. Binary Search Tree (BST)

Type: Tree
Variants: Self-balancing BSTs like AVL Tree, Red-Black Tree
Time Complexity:
- Insertion: O(log n) (for balanced trees)
- Deletion: O(log n) (for balanced trees)
- Peek (Find-Min/Find-Max): O(log n) (for balanced trees)
Pros:
- Allows for all priority queue operations with logarithmic time complexity.
- Provides sorted order traversal, which might be useful in some applications.
Cons:
- More complex to implement than heaps.
- Insertions and deletions are more computationally expensive due to the need to maintain balance.

3. Fibonacci Heap

Type: Heap
Time Complexity:
- Insertion: O(1)
- Deletion (Extract-Min): O(log n)
- Decrease-Key: O(1)
- Peek: O(1)
Pros:
- Very efficient for algorithms like Dijkstra's shortest path, where the decrease-key operation is frequent.
Cons:
- More complex to implement compared to binary heaps.
- Higher constant factors can make it less efficient in practice for some scenarios.

4. Unordered List

Type: List/Array
Time Complexity:
- Insertion: O(1)
- Deletion (Extract-Min/Extract-Max): O(n) (requires linear search)
- Peek: O(n)
Pros:
- Very easy to implement.
Cons:
- Inefficient for priority queue operations, especially for large datasets.

5. Ordered List

Type: List/Array
Time Complexity:
- Insertion: O(n) (requires shifting elements to maintain order)
- Deletion (Extract-Min/Extract-Max): O(1)
- Peek: O(1)
Pros:
- Provides quick access to the element with the highest priority.
Cons:
- Insertion is inefficient due to the need to maintain order.

6. Pairing Heap

Type: Heap
Time Complexity:
- Insertion: O(1)
- Deletion (Extract-Min): O(log n)
- Decrease-Key: Amortized O(1)
Pros:
- Simpler than Fibonacci heaps with similar time complexity.
Cons:
- Less known and understood than binary heaps or Fibonacci heaps.

Binary Heap is the most common and practical choice for implementing a priority queue due to its balanced performance across operations and relatively simple implementation.

Fibonacci Heaps are theoretically more efficient for certain operations but are complex to implement.

Binary Search Trees can be used when you need additional operations like range queries or ordered traversal.

Unordered or Ordered Lists are simple but generally inefficient for large datasets.

In most cases, binary heaps (either as a min-heap or max-heap) are recommended for implementing priority queues because they provide a good balance between performance and ease of implementation.

Priority Queue Implementation

We will be implementing Max-Priority Queue using max-heap. To implement Min-priority queue simply use min-heap.

Python

class PriorityQueueNode:
    def __init__(self, priority, value):
        self.priority = priority
        self.value = value

class PriorityQueue:
    def __init__(self):
        # Initialize an empty list to store the queue elements
        self.pq = []

    def is_empty(self):
        # Check if the queue is empty
        return len(self.pq) == 0

    def insert(self, priority, value):
        # Insert the item into the queue
        node = PriorityQueueNode(priority, value)
        self.pq.append(node)
        self._percolate_up(len(self.pq) - 1)

    def _percolate_up(self, index):
        # Move the element at the given index up the heap to maintain the heap property
        parent_index = (index - 1) // 2
        while index > 0 and self.pq[index].priority > self.pq[parent_index].priority:
            # Swap the current element with its parent if it's greater
            self.pq[index], self.pq[parent_index] = (
                self.pq[parent_index],
                self.pq[index],
            )
            index = parent_index
            parent_index = (index - 1) // 2

    def get_max(self):
        # Remove and return the maximum element from the queue (root of the heap)
        if self.is_empty():
            raise IndexError("get_max from empty queue")

        if len(self.pq) == 1:
            return self.pq.pop()

        root = self.pq[0]
        # Move the last element to the root and percolate down
        self.pq[0] = self.pq.pop()
        self._percolate_down(0)

        return root

    def _percolate_down(self, index):
        # Move the element at the given index down the heap to maintain the heap property
        size = len(self.pq)
        largest = index
        left = 2 * index + 1
        right = 2 * index + 2

        # Check if the left child exists and is greater than the current element
        if left < size and self.pq[left].priority > self.pq[largest].priority:
            largest = left

        # Check if the right child exists and is greater than the current largest
        if right < size and self.pq[right].priority > self.pq[largest].priority:
            largest = right

        # If the largest element is not the current element, swap and continue percolating down
        if largest != index:
            self.pq[index], self.pq[largest] = (
                self.pq[largest],
                self.pq[index],
            )
            self._percolate_down(largest)

    def peek_max(self):
        # Return the maximum element without removing it
        if self.is_empty():
            raise IndexError("peek_max from empty queue")
        return self.pq[0]

    def size(self):
        # Return the size of the queue
        return len(self.pq)

# Example usage
pq = PriorityQueue()
pq.insert(10, "Task 1")
pq.insert(4, "Task 2")
pq.insert(9, "Task 3")
pq.insert(2, "Task 4")
pq.insert(7, "Task 5")

print("Max priority element:", pq.get_max().value)
print("Max priority element:", pq.get_max().value)
pq.insert(5, "Task 6")
print("Max priority element:", pq.get_max().value)

JavaScript

class PriorityQueueNode {
    constructor(priority, value) {
        this.priority = priority;
        this.value = value;
    }
}

class PriorityQueue {
    constructor() {
        this.pq = [];
    }

    isEmpty() {
        return this.pq.length === 0;
    }

    insert(priority, value) {
        const node = new PriorityQueueNode(priority, value);
        this.pq.push(node);
        this.percolateUp(this.pq.length - 1);
    }

    percolateUp(index) {
        let parentIndex = Math.floor((index - 1) / 2);
        while (index > 0 && this.pq[index].priority > this.pq[parentIndex].priority) {
            [this.pq[index], this.pq[parentIndex]] = [this.pq[parentIndex], this.pq[index]];
            index = parentIndex;
            parentIndex = Math.floor((index - 1) / 2);
        }
    }

    getMax() {
        if (this.isEmpty()) {
            throw new Error("getMax from empty queue");
        }

        if (this.pq.length === 1) {
            return this.pq.pop();
        }

        const root = this.pq[0];
        this.pq[0] = this.pq.pop();
        this.percolateDown(0);

        return root;
    }

    percolateDown(index) {
        const size = this.pq.length;
        let largest = index;
        const left = 2 * index + 1;
        const right = 2 * index + 2;

        if (left < size && this.pq[left].priority > this.pq[largest].priority) {
            largest = left;
        }

        if (right < size && this.pq[right].priority > this.pq[largest].priority) {
            largest = right;
        }

        if (largest !== index) {
            [this.pq[index], this.pq[largest]] = [this.pq[largest], this.pq[index]];
            this.percolateDown(largest);
        }
    }

    peekMax() {
        if (this.isEmpty()) {
            throw new Error("peekMax from empty queue");
        }
        return this.pq[0];
    }

    size() {
        return this.pq.length;
    }
}

// Example usage
const pq = new PriorityQueue();
pq.insert(10, "Task 1");
pq.insert(4, "Task 2");
pq.insert(9, "Task 3");
pq.insert(2, "Task 4");
pq.insert(7, "Task 5");

console.log("Max priority element:", pq.getMax().value);
console.log("Max priority element:", pq.getMax().value);
pq.insert(5, "Task 6");
console.log("Max priority element:", pq.getMax().value);

Java

import java.util.ArrayList;

class PriorityQueueNode {
    int priority;
    String value;

    public PriorityQueueNode(int priority, String value) {
        this.priority = priority;
        this.value = value;
    }
}

class PriorityQueue {
    private ArrayList<PriorityQueueNode> pq;

    public PriorityQueue() {
        pq = new ArrayList<>();
    }

    public boolean isEmpty() {
        return pq.isEmpty();
    }

    public void insert(int priority, String value) {
        PriorityQueueNode node = new PriorityQueueNode(priority, value);
        pq.add(node);
        percolateUp(pq.size() - 1);
    }

    private void percolateUp(int index) {
        int parentIndex = (index - 1) / 2;
        while (index > 0 && pq.get(index).priority > pq.get(parentIndex).priority) {
            swap(index, parentIndex);
            index = parentIndex;
            parentIndex = (index - 1) / 2;
        }
    }

    public PriorityQueueNode getMax() {
        if (isEmpty()) {
            throw new IndexOutOfBoundsException("getMax from empty queue");
        }

        if (pq.size() == 1) {
            return pq.remove(pq.size() - 1);
        }

        PriorityQueueNode root = pq.get(0);
        pq.set(0, pq.remove(pq.size() - 1));
        percolateDown(0);

        return root;
    }

    private void percolateDown(int index) {
        int size = pq.size();
        int largest = index;
        int left = 2 * index + 1;
        int right = 2 * index + 2;

        if (left < size && pq.get(left).priority > pq.get(largest).priority) {
            largest = left;
        }

        if (right < size && pq.get(right).priority > pq.get(largest).priority) {
            largest = right;
        }

        if (largest != index) {
            swap(index, largest);
            percolateDown(largest);
        }
    }

    public PriorityQueueNode peekMax() {
        if (isEmpty()) {
            throw new IndexOutOfBoundsException("peekMax from empty queue");
        }
        return pq.get(0);
    }

    public int size() {
        return pq.size();
    }

    private void swap(int i, int j) {
        PriorityQueueNode temp = pq.get(i);
        pq.set(i, pq.get(j));
        pq.set(j, temp);
    }

    // Example usage
    public static void main(String[] args) {
        PriorityQueue pq = new PriorityQueue();
        pq.insert(10, "Task 1");
        pq.insert(4, "Task 2");
        pq.insert(9, "Task 3");
        pq.insert(2, "Task 4");
        pq.insert(7, "Task 5");

        System.out.println("Max priority element: " + pq.getMax().value);
        System.out.println("Max priority element: " + pq.getMax().value);
        pq.insert(5, "Task 6");
        System.out.println("Max priority element: " + pq.getMax().value);
    }
}

package main

import (
	"errors"
	"fmt"
)

type PriorityQueueNode struct {
	priority int
	value    string
}

type PriorityQueue struct {
	pq []PriorityQueueNode
}

func NewPriorityQueue() *PriorityQueue {
	return &PriorityQueue{
		pq: []PriorityQueueNode{},
	}
}

func (pq *PriorityQueue) isEmpty() bool {
	return len(pq.pq) == 0
}

func (pq *PriorityQueue) insert(priority int, value string) {
	node := PriorityQueueNode{priority: priority, value: value}
	pq.pq = append(pq.pq, node)
	pq.percolateUp(len(pq.pq) - 1)
}

func (pq *PriorityQueue) percolateUp(index int) {
	parentIndex := (index - 1) / 2
	for index > 0 && pq.pq[index].priority > pq.pq[parentIndex].priority {
		pq.pq[index], pq.pq[parentIndex] = pq.pq[parentIndex], pq.pq[index]
		index = parentIndex
		parentIndex = (index - 1) / 2
	}
}

func (pq *PriorityQueue) getMax() (PriorityQueueNode, error) {
	if pq.isEmpty() {
		return PriorityQueueNode{}, errors.New("getMax from empty queue")
	}

	if len(pq.pq) == 1 {
		node := pq.pq[0]
		pq.pq = pq.pq[:0]
		return node, nil
	}

	root := pq.pq[0]
	pq.pq[0] = pq.pq[len(pq.pq)-1]
	pq.pq = pq.pq[:len(pq.pq)-1]
	pq.percolateDown(0)

	return root, nil
}

func (pq *PriorityQueue) percolateDown(index int) {
	size := len(pq.pq)
	largest := index
	left := 2*index + 1
	right := 2*index + 2

	if left < size && pq.pq[left].priority > pq.pq[largest].priority {
		largest = left
	}

	if right < size && pq.pq[right].priority > pq.pq[largest].priority {
		largest = right
	}

	if largest != index {
		pq.pq[index], pq.pq[largest] = pq.pq[largest], pq.pq[index]
		pq.percolateDown(largest)
	}
}

func (pq *PriorityQueue) peekMax() (PriorityQueueNode, error) {
	if pq.isEmpty() {
		return PriorityQueueNode{}, errors.New("peekMax from empty queue")
	}
	return pq.pq[0], nil
}

func (pq *PriorityQueue) size() int {
	return len(pq.pq)
}

func main() {
	pq := NewPriorityQueue()
	pq.insert(10, "Task 1")
	pq.insert(4, "Task 2")
	pq.insert(9, "Task 3")
	pq.insert(2, "Task 4")
	pq.insert(7, "Task 5")

	if max, err := pq.getMax(); err == nil {
		fmt.Println("Max priority element:", max.value)
	}
	if max, err := pq.getMax(); err == nil {
		fmt.Println("Max priority element:", max.value)
	}
	pq.insert(5, "Task 6")
	if max, err := pq.getMax(); err == nil {
		fmt.Println("Max priority element:", max.value)
	}
}

#include <iostream>
#include <vector>
#include <stdexcept>

class PriorityQueueNode {
public:
    int priority;
    std::string value;

    PriorityQueueNode(int p, const std::string &v) : priority(p), value(v) {}
};

class PriorityQueue {
private:
    std::vector<PriorityQueueNode> pq;

    void percolateUp(int index) {
        int parentIndex = (index - 1) / 2;
        while (index > 0 && pq[index].priority > pq[parentIndex].priority) {
            std::swap(pq[index], pq[parentIndex]);
            index = parentIndex;
            parentIndex = (index - 1) / 2;
        }
    }

    void percolateDown(int index) {
        int size = pq.size();
        int largest = index;
        int left = 2 * index + 1;
        int right = 2 * index + 2;

        if (left < size && pq[left].priority > pq[largest].priority) {
            largest = left;
        }

        if (right < size && pq[right].priority > pq[largest].priority) {
            largest = right;
        }

        if (largest != index) {
            std::swap(pq[index], pq[largest]);
            percolateDown(largest);
        }
    }

public:
    bool isEmpty() const {
        return pq.empty();
    }

    void insert(int priority, const std::string &value) {
        pq.emplace_back(priority, value);
        percolateUp(pq.size() - 1);
    }

    PriorityQueueNode getMax() {
        if (isEmpty()) {
            throw std::out_of_range("getMax from empty queue");
        }

        if (pq.size() == 1) {
            PriorityQueueNode root = pq.back();
            pq.pop_back();
            return root;
        }

        PriorityQueueNode root = pq[0];
        pq[0] = pq.back();
        pq.pop_back();
        percolateDown(0);

        return root;
    }

    PriorityQueueNode peekMax() const {
        if (isEmpty()) {
            throw std::out_of_range("peekMax from empty queue");
        }
        return pq[0];
    }

    int size() const {
        return pq.size();
    }
};

int main() {
    PriorityQueue pq;
    pq.insert(10, "Task 1");
    pq.insert(4, "Task 2");
    pq.insert(9, "Task 3");
    pq.insert(2, "Task 4");
    pq.insert(7, "Task 5");

    std::cout << "Max priority element: " << pq.getMax().value << std::endl;
    std::cout << "Max priority element: " << pq.getMax().value << std::endl;
    pq.insert(5, "Task 6");
    std::cout << "Max priority element: " << pq.getMax().value << std::endl;

    return 0;
}

Rust

#[derive(Debug, Clone)]
struct PriorityQueueNode {
    priority: i32,
    value: String,
}

struct PriorityQueue {
    pq: Vec<PriorityQueueNode>,
}

impl PriorityQueue {
    fn new() -> Self {
        Self { pq: Vec::new() }
    }

    fn is_empty(&self) -> bool {
        self.pq.is_empty()
    }

    fn insert(&mut self, priority: i32, value: String) {
        let node = PriorityQueueNode { priority, value };
        self.pq.push(node);
        self.percolate_up(self.pq.len() - 1);
    }

    fn percolate_up(&mut self, index: usize) {
        let mut index = index;
        while index > 0 {
            let parent_index = (index - 1) / 2;
            if self.pq[index].priority > self.pq[parent_index].priority {
                self.pq.swap(index, parent_index);
                index = parent_index;
            } else {
                break;
            }
        }
    }

    fn get_max(&mut self) -> Result<PriorityQueueNode, String> {
        if self.is_empty() {
            return Err("get_max from empty queue".to_string());
        }

        if self.pq.len() == 1 {
            return Ok(self.pq.pop().unwrap());
        }

        let root = self.pq[0].clone();
        self.pq[0] = self.pq.pop().unwrap();
        self.percolate_down(0);

        Ok(root)
    }

    fn percolate_down(&mut self, index: usize) {
        let size = self.pq.len();
        let mut largest = index;
        let left = 2 * index + 1;
        let right = 2 * index + 2;

        if left < size && self.pq[left].priority > self.pq[largest].priority {
            largest = left;
        }

        if right < size && self.pq[right].priority > self.pq[largest].priority {
            largest = right;
        }

        if largest != index {
            self.pq.swap(index, largest);
            self.percolate_down(largest);
        }
    }

    fn peek_max(&self) -> Result<&PriorityQueueNode, String> {
        if self.is_empty() {
            return Err("peek_max from empty queue".to_string());
        }
        Ok(&self.pq[0])
    }

    fn size(&self) -> usize {
        self.pq.len()
    }
}

fn main() {
    let mut pq = PriorityQueue::new();
    pq.insert(10, "Task 1".to_string());
    pq.insert(4, "Task 2".to_string());
    pq.insert(9, "Task 3".to_string());
    pq.insert(2, "Task 4".to_string());
    pq.insert(7, "Task 5".to_string());

    println!("Max priority element: {:?}", pq.get_max().unwrap().value);
    println!("Max priority element: {:?}", pq.get_max().unwrap().value);
    pq.insert(5, "Task 6".to_string());
    println!("Max priority element: {:?}", pq.get_max().unwrap().value);
}

Output

Max priority element: Task 1
Max priority element: Task 3
Max priority element: Task 5

Applications of Priority Queues

CPU Scheduling: Operating systems use priority queues to manage processes based on their priority. Higher-priority tasks are given more CPU time.
Dijkstra's Algorithm: This algorithm for finding the shortest path in a graph uses a priority queue to always extend the shortest known path first.
Huffman Coding: A priority queue is used to build the optimal prefix code for data compression in the Huffman coding algorithm.
Event Simulation: In simulations, events are often scheduled to occur at various times. A priority queue can manage these events by their time of occurrence.

Time Complexity

The time complexity of various operations on a priority queue depends on the underlying data structure:

Insertion: O(log n) — due to the need to maintain the heap property.
Deletion: O(log n) — for removing the root element and reheapifying.
Peek: O(1) — the top element of the heap is directly accessible.
Build Heap: O(n) — for converting an unsorted array into a heap.

Priority Queue

Key Concepts of Priority Queues

Types of Priority Queues

Operations on a Priority Queue

Which data structure to use for Priority Queue?

1. Binary Heap

2. Binary Search Tree (BST)

3. Fibonacci Heap

4. Unordered List

5. Ordered List

6. Pairing Heap

Priority Queue Implementation

Applications of Priority Queues

Time Complexity

Recommended Posts