Introduction to Trees

Abhishek Kumar • Category: Data Structures • Tags: datastructures tree

---

A tree is a non-linear data structures in which each node can point to a number of nodes. A tree can be used to represent the hierarchy of data in graphical form.

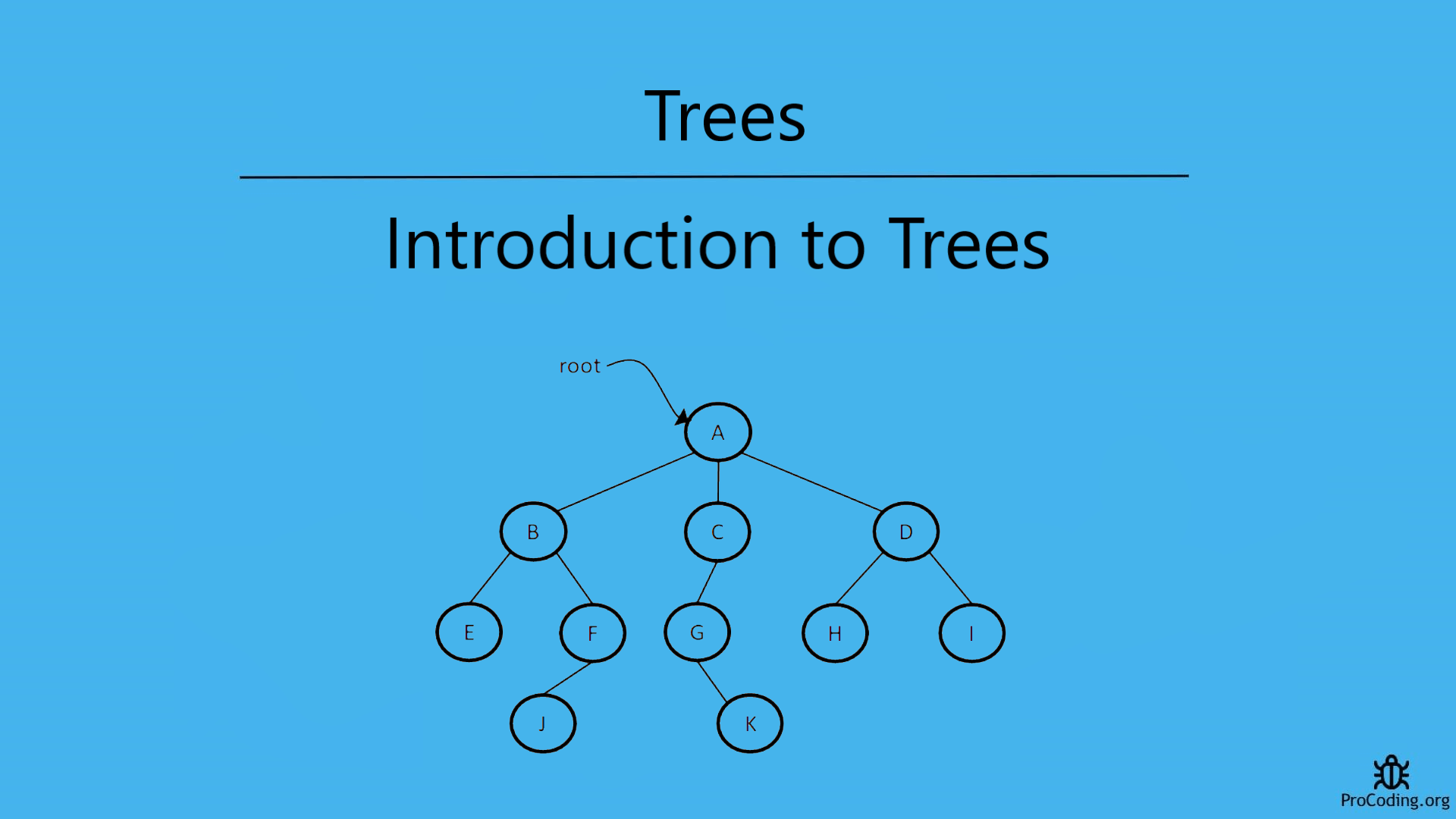
In trees, the order of elements is not important. If ordering is required then linear data structures should be used like an array, linked list, stack etc.

Important points related to Trees

• Root: The root of a tree is the node with no parents. There can be at most one root node. (node A is the root)
• Edge: An edge refers to the link from one node to another node. (all the links in the image)
• Leaf node: A node with no children in called leaf. (E, J, K, H, I)
• Siblings: Children of same parent are called siblings. (B, C, D are siblings of parent A, E and F are siblings of parent B)
• Ancestor and Descendant: A node p is ancestor of q if p appears on the path from root to q and q is descendant of p. (A, C, D are ancestor of K)
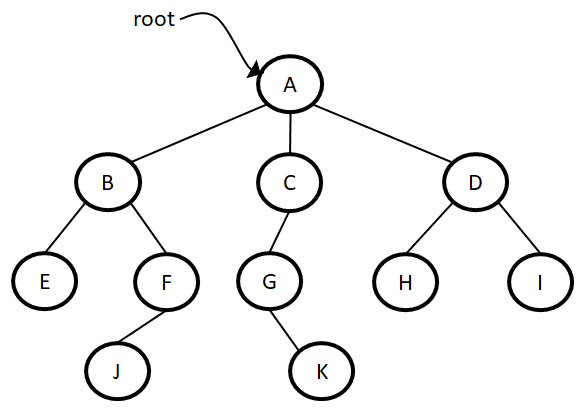
• Level: The set of all nodes at a given depth is called level of the tree.
  
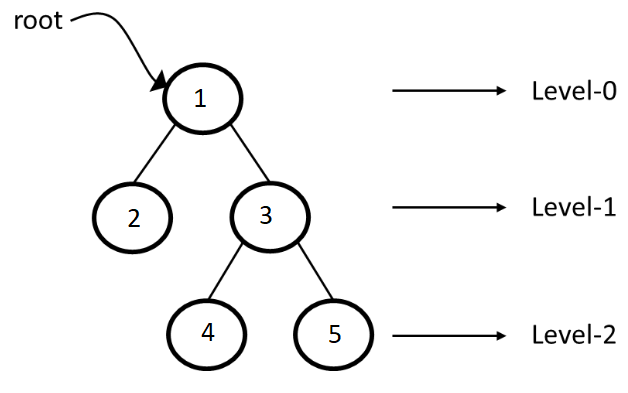
• Depth: The depth of a node is the length of the path from root to the node. (depth of G is 2, A – C - G)
• Height of a node: The height of a node is the length of the path from that node to the deepest node. (Height of node B is 2 i.e., B – F – J)
• Height of a tree: The height of a tree is the length of the path from root node to the deepest node in the tree. So, the tree with only one node has a height of 0. (Height of node B is 3 i.e., A – C - G – K or A – B – F – J)
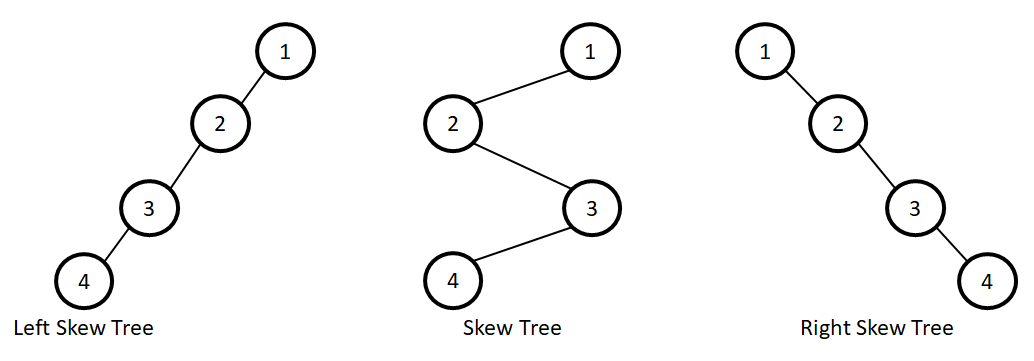
• Skew tree: Tree in which each node only has either left child or right child is known as Skew tree.
  

Types of trees

1. Binary Tree *
2. N-Ary Tree
3. Threaded Binary Tree
4. XOR Tree
5. Binary Search Tree *
6. AVL Tree *
7. Red-Black Tree *
8. Splay Tree
9. B-Tree *

There are some trees other than this also but these are the most common trees and the type of trees marked with * are the most important one.

All the trees have their specific way of inserting, deleting data and for other operations also. So we will be talking about them in their specific sections.

---