Heapify
Explore the concept of heapify with in-depth explanations on converting arrays into min heaps and max heaps. This comprehensive guide covers both iterative and recursive implementations across multiple programming languages, including Python, JavaScript, Java, C++, Go, and Rust, with detailed code examples and explanations to enhance your understanding of heap data structures.
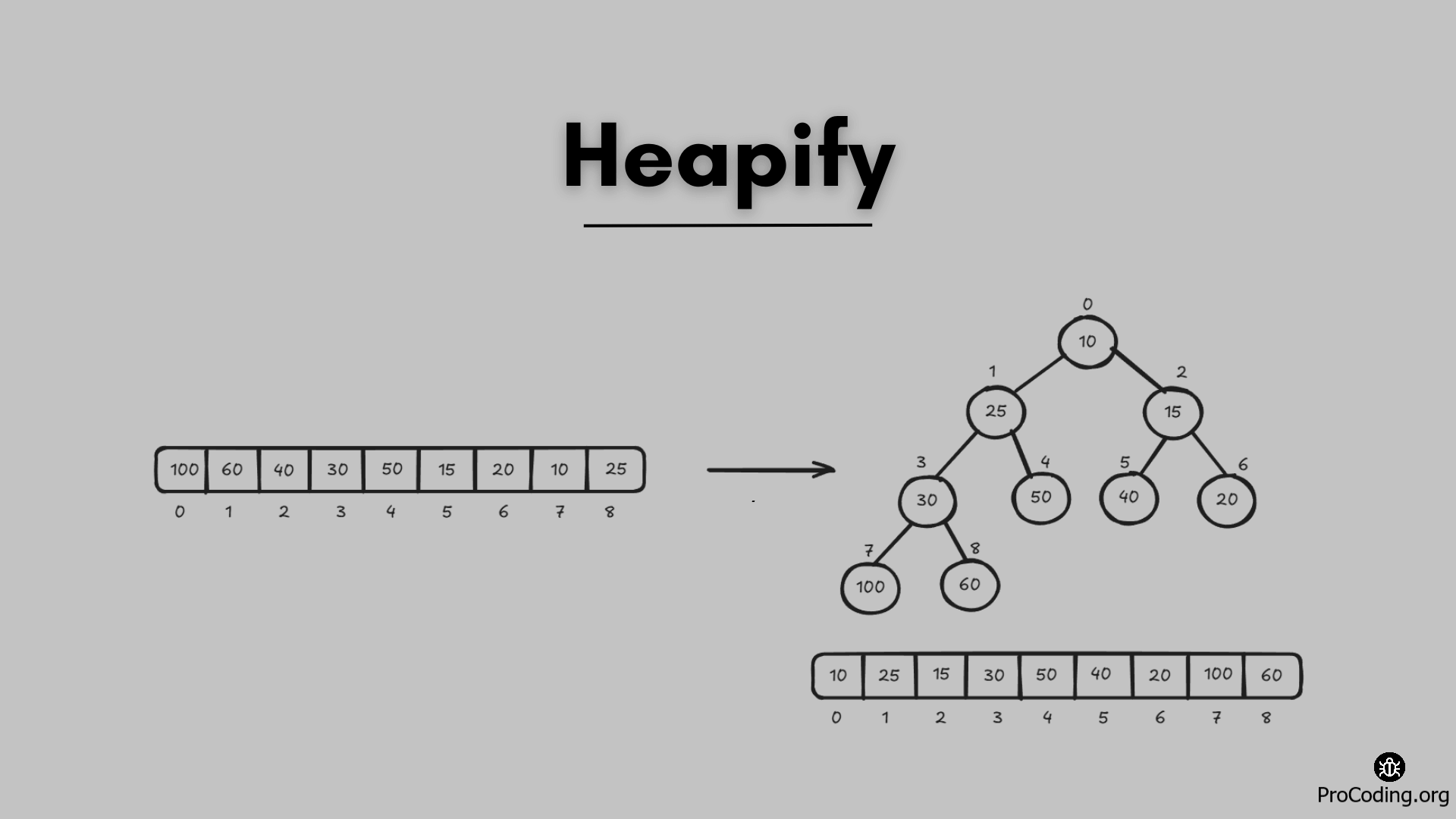
Table of contents
We have studied creating min-heap and max-heap from scratch. But there will be many cases when we already have an array and we have to create a heap out of it.
One simple way is to read all data one by one and put them into the new heap. Since the insertion of one element takes O(log n) time so we have to insert n elements the overall time complexity in the worst case will be O(n log n).
We can further optimize creating a new heap if we already have an array using the Heapify method.
Heapify
Heapify is a process used to convert an array into a heap, which is a specific type of binary tree data structure. A heap can be either a min heap or a max heap:
- Min Heap: In a min heap, the parent node is always smaller than or equal to its child nodes. The smallest element is at the root of the tree.
- Max Heap: In a max heap, the parent node is always larger than or equal to its child nodes. The largest element is at the root of the tree.
The terms "heapify", "heapify down" and “heapify up” are related but refer to different concepts or processes within the context of heaps, specifically in how an array is organized to maintain heap properties.
- Heapify is a broader term used to describe the process of converting an entire array into a heap, whether it's a min-heap or a max-heap.
- Heapify down is a specific operation used to maintain the heap property after the root of the heap has been removed or replaced.
- Heapify up used to restore the heap property after inserting a new element into the heap.
Heapify down is also known as percolate down, sift down and bubble down. And Heapify up is also known as percolate up, sift up and bubble up.
These terms can be used interchangeably so do not get confused. To understand it better read these -
Heapify down and Heapify up are not the same as Heapify.
Min heapify
To get a min-heap from a given we will use Min heapify algorithms and to understand heapify method let's try to convert a given array and transform it into min-heap.
Let's take an example of this array -
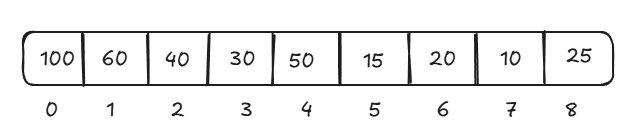
The tree representation of this array will be like this -
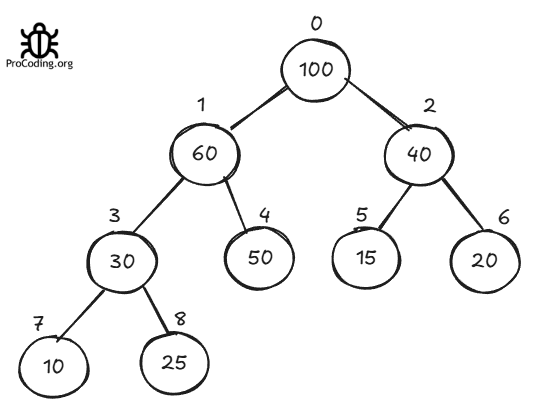
For heapify, we must ignore leaf nodes and perform operations only on the non-leaf nodes. Leaf nodes will be handled while operating on their parents.
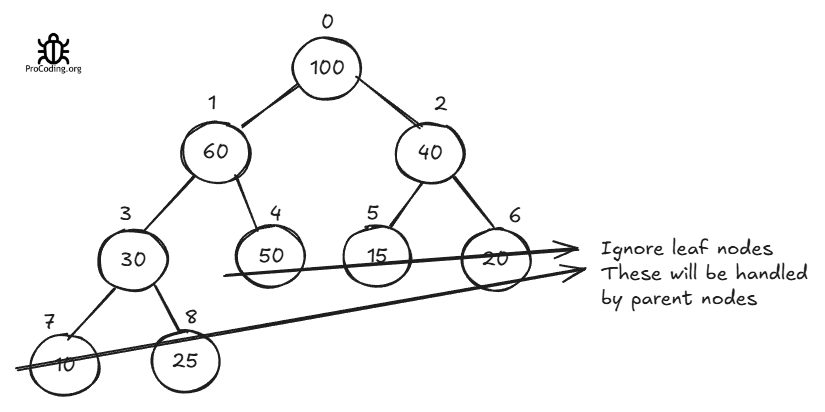
By the property of binary tree, there will always be n/2 number of leaf nodes. So, we have to work only on the remaining n/2 nodes.
And this operation will be performed in reverse order i.e., from n/2 to 0
Now, let's understand about the operation.
We have to go through each non-leaf node compare its value with its children and make the minimum value the root node (for max-heap make the maximum as root). Basically, for each node with children make sure they are following heap property.
If they are following a heap property then do nothing otherwise change the root.
For example (for min-heap):

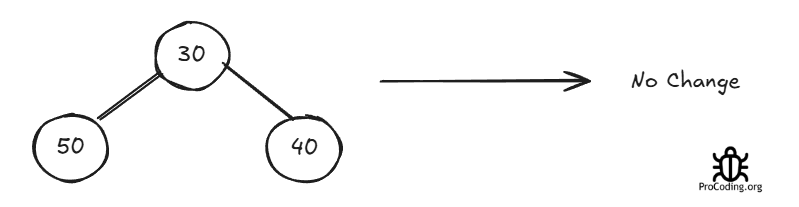
Okay Now let's try to create a min-heap using the Heapify method from the array we have. Start with the first non-leaf node 30-
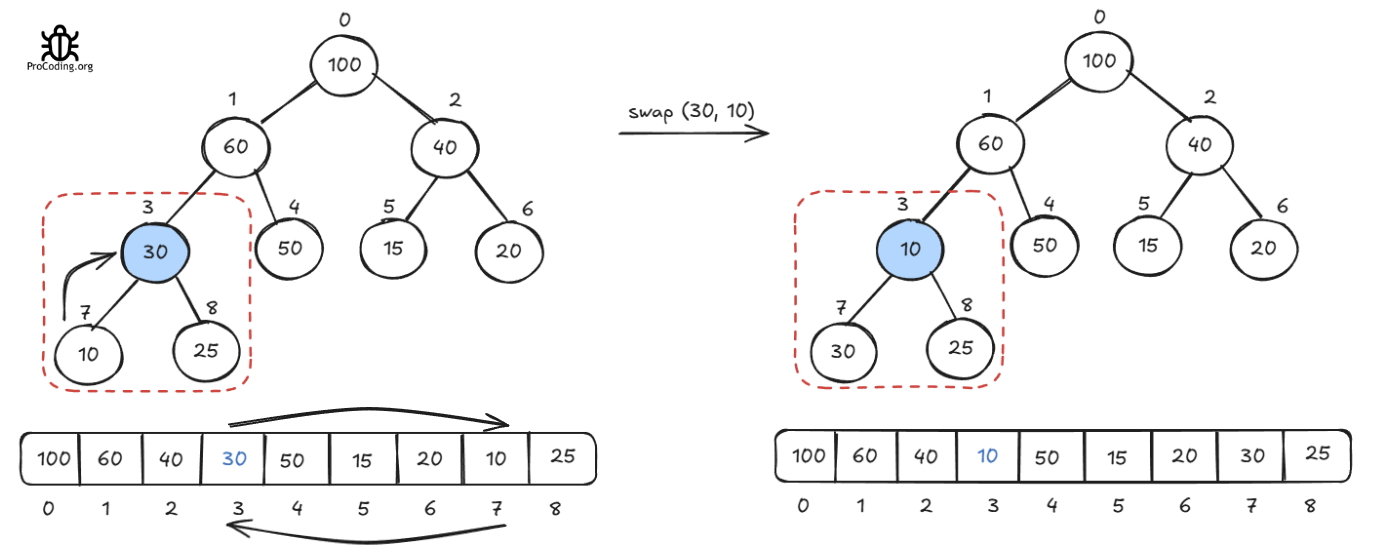
Let's see the next non-leaf node 40
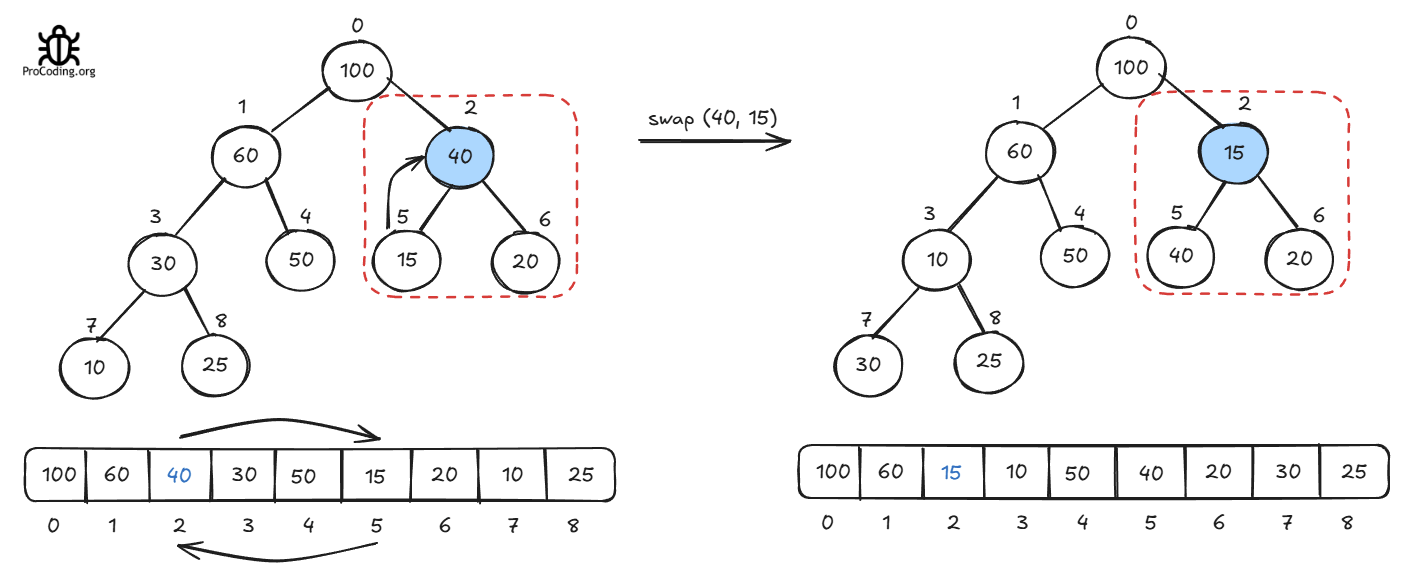
Next non-leaf node 60, After moving 60 downwards new position is also disturbed so further move this
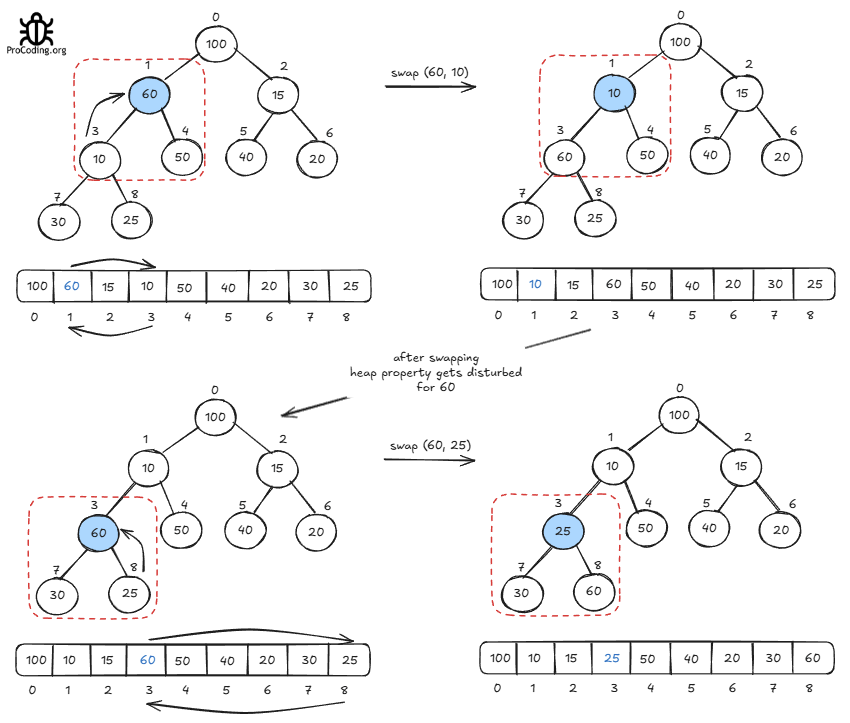
The next non-leaf node is the root node 100
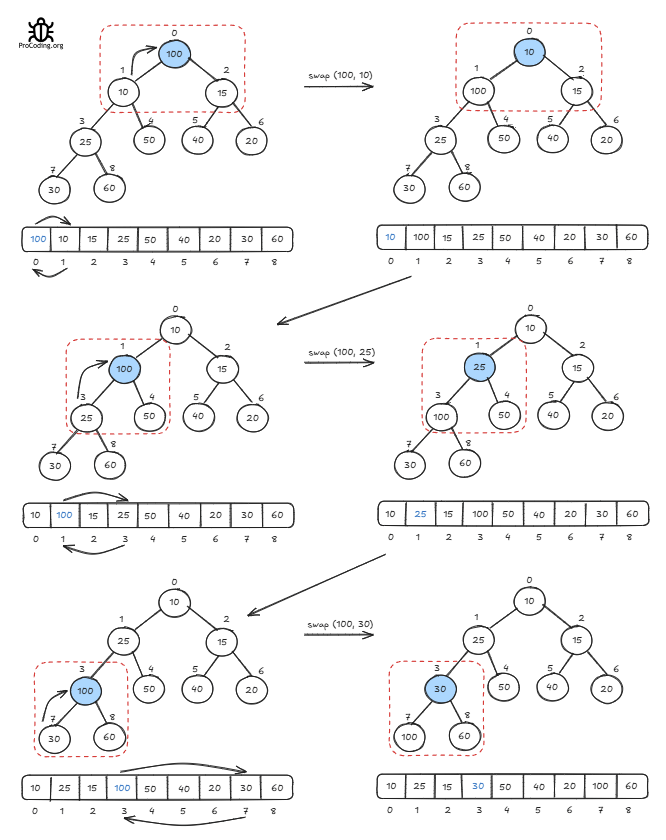
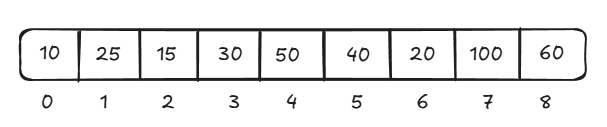
After converting an array into the heap, the array will be like
And its tree representation will be
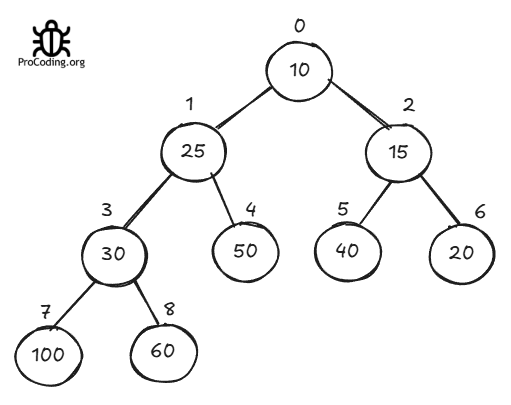
By using heapify method we want to make sure each node is following heap property and minimum element will be at root of tree (at 0th index)
Min heapify code - recursive
Python
def heapify_helper(arr, n, i):
smallest = i
left = 2 * i + 1
right = 2 * i + 2
# If the left child is smaller than the current smallest
if left < n and arr[left] < arr[smallest]:
smallest = left
# If the right child is smaller than the current smallest
if right < n and arr[right] < arr[smallest]:
smallest = right
# If the smallest is not the root
if smallest != i:
arr[i], arr[smallest] = arr[smallest], arr[i] # Swap
heapify_helper(arr, n, smallest) # Recursively heapify the affected subtree
def heapify(arr):
n = len(arr)
# Build the min heap by calling heapify for all non-leaf nodes
for i in range(n // 2 - 1, -1, -1):
heapify_helper(arr, n, i)
arr = [100, 60, 40, 30, 50, 15, 20, 10, 25]
print(arr)
JavaScript
function heapifyHelper(arr, n, i) {
let smallest = i;
let left = 2 * i + 1;
let right = 2 * i + 2;
// If the left child is smaller than the current smallest
if (left < n && arr[left] < arr[smallest]) {
smallest = left;
}
// If the right child is smaller than the current smallest
if (right < n && arr[right] < arr[smallest]) {
smallest = right;
}
// If the smallest is not the root
if (smallest !== i) {
[arr[i], arr[smallest]] = [arr[smallest], arr[i]]; // Swap
// Recursively heapify the affected subtree
heapifyHelper(arr, n, smallest);
}
}
function heapify(arr) {
let n = arr.length;
// Build the min heap by calling heapify for all non-leaf nodes
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
let arr = [100, 60, 40, 30, 50, 15, 20, 10, 25];
console.log("Original array:", arr);
heapify(arr);
console.log("Heapified array:", arr);
Java
public class MinHeap {
public static void heapifyHelper(int[] arr, int n, int i) {
int smallest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// If the left child is smaller than the current smallest
if (left < n && arr[left] < arr[smallest]) {
smallest = left;
}
// If the right child is smaller than the current smallest
if (right < n && arr[right] < arr[smallest]) {
smallest = right;
}
// If the smallest is not the root
if (smallest != i) {
int temp = arr[i];
arr[i] = arr[smallest];
arr[smallest] = temp;
// Recursively heapify the affected subtree
heapifyHelper(arr, n, smallest);
}
}
public static void heapify(int[] arr) {
int n = arr.length;
// Build the min heap by calling heapify for all non-leaf nodes
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
public static void main(String[] args) {
int[] arr = {100, 60, 40, 30, 50, 15, 20, 10, 25};
System.out.println("Original array:");
for (int i : arr) {
System.out.print(i + " ");
}
heapify(arr);
System.out.println("\nHeapified array:");
for (int i : arr) {
System.out.print(i + " ");
}
}
}
Go
package main
import (
"fmt"
)
func heapifyHelper(arr []int, n int, i int) {
smallest := i
left := 2*i + 1
right := 2*i + 2
// If the left child is smaller than the current smallest
if left < n && arr[left] < arr[smallest] {
smallest = left
}
// If the right child is smaller than the current smallest
if right < n && arr[right] < arr[smallest] {
smallest = right
}
// If the smallest is not the root
if smallest != i {
arr[i], arr[smallest] = arr[smallest], arr[i] // Swap
// Recursively heapify the affected subtree
heapifyHelper(arr, n, smallest)
}
}
func heapify(arr []int) {
n := len(arr)
// Build the min heap by calling heapify for all non-leaf nodes
for i := n/2 - 1; i >= 0; i-- {
heapifyHelper(arr, n, i)
}
}
func main() {
arr := []int{100, 60, 40, 30, 50, 15, 20, 10, 25}
fmt.Println("Original array:", arr)
heapify(arr)
fmt.Println("Heapified array:", arr)
}
C++
#include <iostream>
#include <vector>
using namespace std;
void heapifyHelper(vector<int>& arr, int n, int i) {
int smallest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// If the left child is smaller than the current smallest
if (left < n && arr[left] < arr[smallest]) {
smallest = left;
}
// If the right child is smaller than the current smallest
if (right < n && arr[right] < arr[smallest]) {
smallest = right;
}
// If the smallest is not the root
if (smallest != i) {
swap(arr[i], arr[smallest]);
// Recursively heapify the affected subtree
heapifyHelper(arr, n, smallest);
}
}
void heapify(vector<int>& arr) {
int n = arr.size();
// Build the min heap by calling heapify for all non-leaf nodes
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
int main() {
vector<int> arr = {100, 60, 40, 30, 50, 15, 20, 10, 25};
cout << "Original array: ";
for (int val : arr) {
cout << val << " ";
}
cout << endl;
heapify(arr);
cout << "Heapified array: ";
for (int val : arr) {
cout << val << " ";
}
cout << endl;
return 0;
}
Rust
fn heapify_helper(arr: &mut Vec<i32>, n: usize, i: usize) {
let mut smallest = i;
let left = 2 * i + 1;
let right = 2 * i + 2;
// If the left child is smaller than the current smallest
if left < n && arr[left] < arr[smallest] {
smallest = left;
}
// If the right child is smaller than the current smallest
if right < n && arr[right] < arr[smallest] {
smallest = right;
}
// If the smallest is not the root
if smallest != i {
arr.swap(i, smallest);
// Recursively heapify the affected subtree
heapify_helper(arr, n, smallest);
}
}
fn heapify(arr: &mut Vec<i32>) {
let n = arr.len();
// Build the min heap by calling heapify for all non-leaf nodes
for i in (0..n / 2).rev() {
heapify_helper(arr, n, i);
}
}
fn main() {
let mut arr = vec![100, 60, 40, 30, 50, 15, 20, 10, 25];
println!("Original array: {:?}", arr);
heapify(&mut arr);
println!("Heapified array: {:?}", arr);
}
Min heapify code - iterative
Python
def heapify(arr):
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
parent = i
left = 2 * parent + 1
right = 2 * parent + 2
while left < n:
min_index = parent
if arr[min_index] > arr[left]: # Use > for min heap
min_index = left
if right < n and arr[min_index] > arr[right]: # Use > for min heap
min_index = right
if min_index == parent:
break
arr[min_index], arr[parent] = arr[parent], arr[min_index]
parent = min_index
left = 2 * parent + 1
right = 2 * parent + 2
arr = [100, 60, 40, 30, 50, 15, 20, 10, 25]
heapify(arr)
print(arr)
JavaScript
function heapify(arr) {
const n = arr.length;
// Start from the last non-leaf node and move upwards in the tree
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
let parent = i;
let left = 2 * parent + 1;
let right = 2 * parent + 2;
while (left < n) {
let minIndex = parent;
// Compare parent with left child
if (arr[minIndex] > arr[left]) {
minIndex = left;
}
// Compare with right child if it exists
if (right < n && arr[minIndex] > arr[right]) {
minIndex = right;
}
// If the parent is already in the correct position, exit loop
if (minIndex === parent) {
break;
}
// Swap the parent with the smaller of its children
[arr[minIndex], arr[parent]] = [arr[parent], arr[minIndex]];
// Move down the tree
parent = minIndex;
left = 2 * parent + 1;
right = 2 * parent + 2;
}
}
}
const arr = [100, 60, 40, 30, 50, 15, 20, 10, 25];
heapify(arr);
console.log(arr);
Java
public class MinHeap {
public static void heapify(int[] arr) {
int n = arr.length;
// Start from the last non-leaf node and move upwards in the tree
for (int i = n / 2 - 1; i >= 0; i--) {
int parent = i;
while (parent < n) {
int left = 2 * parent + 1;
int right = 2 * parent + 2;
int minIndex = parent;
// Compare parent with left child
if (left < n && arr[minIndex] > arr[left]) {
minIndex = left;
}
// Compare with right child if it exists
if (right < n && arr[minIndex] > arr[right]) {
minIndex = right;
}
// If the parent is not the smallest, swap and continue heapifying
if (minIndex != parent) {
int temp = arr[parent];
arr[parent] = arr[minIndex];
arr[minIndex] = temp;
// Move down to the new minIndex position
parent = minIndex;
} else {
break; // The heap property is satisfied
}
}
}
}
public static void main(String[] args) {
int[] arr = {100, 60, 40, 30, 50, 15, 20, 10, 25};
heapify(arr);
// Print the heapified array
for (int value : arr) {
System.out.print(value + " ");
}
}
}
Go
package main
import "fmt"
// heapify transforms an array into a min-heap
func heapify(arr []int) {
n := len(arr)
// Start from the last non-leaf node and move upwards
for i := n/2 - 1; i >= 0; i-- {
parent := i
for {
left := 2*parent + 1
right := 2*parent + 2
minIndex := parent
// Compare parent with left child
if left < n && arr[minIndex] > arr[left] {
minIndex = left
}
// Compare with right child if it exists
if right < n && arr[minIndex] > arr[right] {
minIndex = right
}
// If the parent is not the smallest, swap and continue heapifying
if minIndex != parent {
arr[minIndex], arr[parent] = arr[parent], arr[minIndex]
parent = minIndex
} else {
break // The heap property is satisfied
}
}
}
}
func main() {
arr := []int{100, 60, 40, 30, 50, 15, 20, 10, 25}
heapify(arr)
// Print the heapified array
for _, value := range arr {
fmt.Print(value, " ")
}
}
C++
#include <iostream>
#include <vector>
using namespace std;
void heapify(vector<int>& arr) {
int n = arr.size();
// Start from the last non-leaf node and move upwards
for (int i = n / 2 - 1; i >= 0; i--) {
int parent = i;
while (true) {
int left = 2 * parent + 1;
int right = 2 * parent + 2;
int minIndex = parent;
// Compare parent with left child
if (left < n && arr[minIndex] > arr[left]) {
minIndex = left;
}
// Compare with right child if it exists
if (right < n && arr[minIndex] > arr[right]) {
minIndex = right;
}
// If the parent is not the smallest, swap and continue heapifying
if (minIndex != parent) {
swap(arr[minIndex], arr[parent]);
parent = minIndex;
} else {
break; // The heap property is satisfied
}
}
}
}
int main() {
vector<int> arr = {100, 60, 40, 30, 50, 15, 20, 10, 25};
heapify(arr);
// Print the heapified array
for (int value : arr) {
cout << value << " ";
}
cout << endl;
return 0;
}
Rust
fn heapify(arr: &mut [i32]) {
let n = arr.len();
// Start from the last non-leaf node and move upwards
for i in (0..n / 2).rev() {
let mut parent = i;
loop {
let left = 2 * parent + 1;
let right = 2 * parent + 2;
let mut min_index = parent;
// Compare parent with left child
if left < n && arr[min_index] > arr[left] {
min_index = left;
}
// Compare with right child if it exists
if right < n && arr[min_index] > arr[right] {
min_index = right;
}
// If the parent is not the smallest, swap and continue heapifying
if min_index != parent {
arr.swap(min_index, parent);
parent = min_index;
} else {
break; // The heap property is satisfied
}
}
}
}
fn main() {
let mut arr = [100, 60, 40, 30, 50, 15, 20, 10, 25];
heapify(&mut arr);
// Print the heapified array
for value in arr.iter() {
print!("{} ", value);
}
println!();
}
Output
10, 25, 15, 30, 50, 40, 20, 100, 60
Max heapify
To create max-heap using a given array all the things are going to be the same the only difference will be in the comparison of data at each step.
At each step, we have to choose max among root, left child and right child and make that as root.

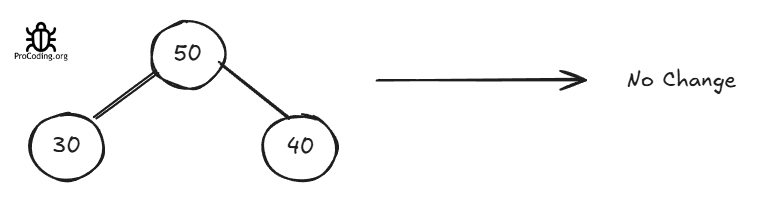
Rest all the things will be same. So will jump directly on the code.
Let's take the example of this array and the result will be -
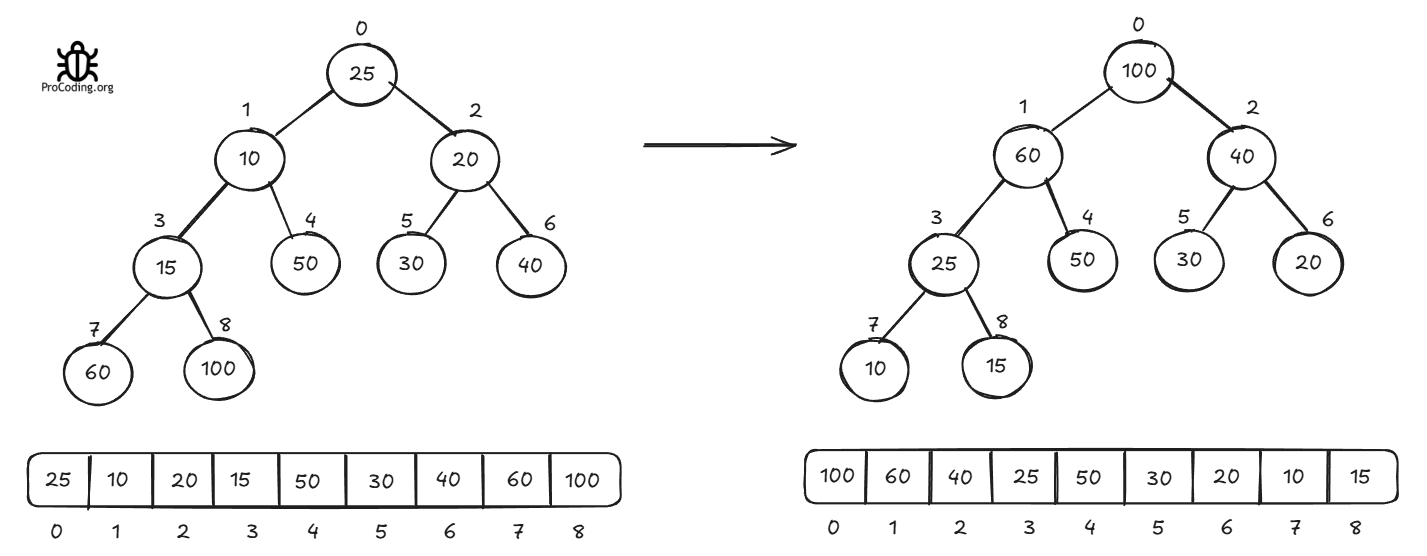
Max heapify code - recursive
Python
def heapify_helper(arr, n, i):
largest = i # Initialize the largest as the root
left = 2 * i + 1 # Left child
right = 2 * i + 2 # Right child
# If the left child exists and is greater than the root
if left < n and arr[left] > arr[largest]:
largest = left
# If the right child exists and is greater than the current largest
if right < n and arr[right] > arr[largest]:
largest = right
# If the largest is not the root, swap and continue heapifying
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # Swap
heapify_helper(arr, n, largest) # Recursively heapify the affected subtree
def heapify(arr):
n = len(arr)
# Build the max heap by calling heapify for all non-leaf nodes
for i in range(n // 2 - 1, -1, -1):
heapify_helper(arr, n, i)
arr = [25, 10, 20, 15, 50, 30, 40, 60, 100]
heapify(arr)
print(arr)
JavaScript
// Helper function to heapify a subtree rooted with node i
function heapifyHelper(arr, n, i) {
let largest = i; // Initialize the largest as the root
let left = 2 * i + 1; // Left child index
let right = 2 * i + 2; // Right child index
// If the left child exists and is greater than the root
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// If the right child exists and is greater than the current largest
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// If the largest is not the root, swap and continue heapifying
if (largest !== i) {
[arr[i], arr[largest]] = [arr[largest], arr[i]]; // Swap
heapifyHelper(arr, n, largest); // Recursively heapify the affected subtree
}
}
// Function to build a max heap
function heapify(arr) {
let n = arr.length;
// Build the max heap by calling heapify for all non-leaf nodes
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
// Example usage
let arr = [25, 10, 20, 15, 50, 30, 40, 60, 100];
heapify(arr);
console.log(arr); // Output the heapified array
Java
public class Heapify {
// Helper function to heapify a subtree rooted with node i
public static void heapifyHelper(int[] arr, int n, int i) {
int largest = i; // Initialize the largest as the root
int left = 2 * i + 1; // Left child index
int right = 2 * i + 2; // Right child index
// If the left child exists and is greater than the root
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// If the right child exists and is greater than the current largest
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// If the largest is not the root, swap and continue heapifying
if (largest != i) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp; // Swap
heapifyHelper(arr, n, largest); // Recursively heapify the affected subtree
}
}
// Function to build a max heap
public static void heapify(int[] arr) {
int n = arr.length;
// Build the max heap by calling heapify for all non-leaf nodes
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
public static void main(String[] args) {
int[] arr = {25, 10, 20, 15, 50, 30, 40, 60, 100};
heapify(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
Go
package main
import "fmt"
// Helper function to heapify a subtree rooted with node i
func heapifyHelper(arr []int, n, i int) {
largest := i // Initialize the largest as the root
left := 2 * i + 1 // Left child index
right := 2 * i + 2 // Right child index
// If the left child exists and is greater than the root
if left < n && arr[left] > arr[largest] {
largest = left
}
// If the right child exists and is greater than the current largest
if right < n && arr[right] > arr[largest] {
largest = right
}
// If the largest is not the root, swap and continue heapifying
if largest != i {
arr[i], arr[largest] = arr[largest], arr[i] // Swap
heapifyHelper(arr, n, largest) // Recursively heapify the affected subtree
}
}
// Function to build a max heap
func heapify(arr []int) {
n := len(arr)
// Build the max heap by calling heapify for all non-leaf nodes
for i := n / 2 - 1; i >= 0; i-- {
heapifyHelper(arr, n, i)
}
}
func main() {
arr := []int{25, 10, 20, 15, 50, 30, 40, 60, 100}
heapify(arr)
fmt.Println(arr) // Output the heapified array
}
C++
#include <iostream>
#include <vector>
void heapifyHelper(std::vector<int>& arr, int n, int i) {
int largest = i; // Initialize the largest as the root
int left = 2 * i + 1; // Left child index
int right = 2 * i + 2; // Right child index
// If the left child exists and is greater than the root
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// If the right child exists and is greater than the current largest
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// If the largest is not the root, swap and continue heapifying
if (largest != i) {
std::swap(arr[i], arr[largest]); // Swap
heapifyHelper(arr, n, largest); // Recursively heapify the affected subtree
}
}
void heapify(std::vector<int>& arr) {
int n = arr.size();
// Build the max heap by calling heapify for all non-leaf nodes
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
int main() {
std::vector<int> arr = {25, 10, 20, 15, 50, 30, 40, 60, 100};
heapify(arr);
for (int num : arr) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Rust
fn heapify_helper(arr: &mut Vec<i32>, n: usize, i: usize) {
let mut largest = i; // Initialize the largest as the root
let left = 2 * i + 1; // Left child index
let right = 2 * i + 2; // Right child index
// If the left child exists and is greater than the root
if left < n && arr[left] > arr[largest] {
largest = left;
}
// If the right child exists and is greater than the current largest
if right < n && arr[right] > arr[largest] {
largest = right;
}
// If the largest is not the root, swap and continue heapifying
if largest != i {
arr.swap(i, largest); // Swap
heapify_helper(arr, n, largest); // Recursively heapify the affected subtree
}
}
fn heapify(arr: &mut Vec<i32>) {
let n = arr.len();
// Build the max heap by calling heapify for all non-leaf nodes
for i in (0..n / 2).rev() {
heapify_helper(arr, n, i);
}
}
fn main() {
let mut arr = vec![25, 10, 20, 15, 50, 30, 40, 60, 100];
heapify(&mut arr);
println!("{:?}", arr); // Output the heapified array
}
Max heapify code - iterative
Python
def heapify(arr):
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
parent = i
left = 2 * parent + 1
right = 2 * parent + 2
while left < n:
max_index = parent
if arr[max_index] < arr[left]: # Use > for max heap
max_index = left
if right < n and arr[max_index] < arr[right]: # Use > for max heap
max_index = right
if max_index == parent:
break
arr[max_index], arr[parent] = arr[parent], arr[max_index]
parent = max_index
left = 2 * parent + 1
right = 2 * parent + 2
arr = [25, 10, 20, 15, 50, 30, 40, 60, 100]
heapify(arr)
print(arr)
JavaScript
function heapify(arr) {
const n = arr.length;
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
let parent = i;
let left = 2 * parent + 1;
let right = 2 * parent + 2;
while (left < n) {
let maxIndex = parent;
if (arr[maxIndex] < arr[left]) { // Use > for max heap
maxIndex = left;
}
if (right < n && arr[maxIndex] < arr[right]) { // Use > for max heap
maxIndex = right;
}
if (maxIndex === parent) {
break;
}
[arr[maxIndex], arr[parent]] = [arr[parent], arr[maxIndex]]; // Swap
parent = maxIndex;
left = 2 * parent + 1;
right = 2 * parent + 2;
}
}
}
const arr = [25, 10, 20, 15, 50, 30, 40, 60, 100];
heapify(arr);
console.log(arr);
Java
import java.util.Arrays;
public class Main {
public static void heapify(int[] arr) {
int n = arr.length;
for (int i = n / 2 - 1; i >= 0; i--) {
int parent = i;
int left = 2 * parent + 1;
int right = 2 * parent + 2;
while (left < n) {
int maxIndex = parent;
if (arr[maxIndex] < arr[left]) { // Use > for max heap
maxIndex = left;
}
if (right < n && arr[maxIndex] < arr[right]) { // Use > for max heap
maxIndex = right;
}
if (maxIndex == parent) {
break;
}
int temp = arr[maxIndex]; // Swap
arr[maxIndex] = arr[parent];
arr[parent] = temp;
parent = maxIndex;
left = 2 * parent + 1;
right = 2 * parent + 2;
}
}
}
public static void main(String[] args) {
int[] arr = {25, 10, 20, 15, 50, 30, 40, 60, 100};
heapify(arr);
System.out.println(Arrays.toString(arr));
}
}
Go
package main
import (
"fmt"
)
func heapify(arr []int) {
n := len(arr)
for i := n/2 - 1; i >= 0; i-- {
parent := i
left := 2*parent + 1
right := 2*parent + 2
for left < n {
maxIndex := parent
if arr[maxIndex] < arr[left] { // Use > for max heap
maxIndex = left
}
if right < n && arr[maxIndex] < arr[right] { // Use > for max heap
maxIndex = right
}
if maxIndex == parent {
break
}
arr[maxIndex], arr[parent] = arr[parent], arr[maxIndex] // Swap
parent = maxIndex
left = 2*parent + 1
right = 2*parent + 2
}
}
}
func main() {
arr := []int{25, 10, 20, 15, 50, 30, 40, 60, 100}
heapify(arr)
fmt.Println(arr)
}
C++
#include <iostream>
#include <vector>
#include <algorithm>
void heapify(std::vector<int>& arr) {
int n = arr.size();
for (int i = n / 2 - 1; i >= 0; i--) {
int parent = i;
int left = 2 * parent + 1;
int right = 2 * parent + 2;
while (left < n) {
int maxIndex = parent;
if (arr[maxIndex] < arr[left]) { // Use > for max heap
maxIndex = left;
}
if (right < n && arr[maxIndex] < arr[right]) { // Use > for max heap
maxIndex = right;
}
if (maxIndex == parent) {
break;
}
std::swap(arr[maxIndex], arr[parent]); // Swap
parent = maxIndex;
left = 2 * parent + 1;
right = 2 * parent + 2;
}
}
}
int main() {
std::vector<int> arr = {25, 10, 20, 15, 50, 30, 40, 60, 100};
heapify(arr);
for (int val : arr) {
std::cout << val << " ";
}
std::cout << std::endl;
return 0;
}
Rust
fn heapify(arr: &mut [i32]) {
let n = arr.len();
for i in (0..n / 2).rev() {
let mut parent = i;
let mut left = 2 * parent + 1;
let mut right = 2 * parent + 2;
while left < n {
let mut max_index = parent;
if arr[max_index] < arr[left] { // Use > for max heap
max_index = left;
}
if right < n && arr[max_index] < arr[right] { // Use > for max heap
max_index = right;
}
if max_index == parent {
break;
}
arr.swap(max_index, parent); // Swap
parent = max_index;
left = 2 * parent + 1;
right = 2 * parent + 2;
}
}
}
fn main() {
let mut arr = vec![25, 10, 20, 15, 50, 30, 40, 60, 100];
heapify(&mut arr);
println!("{:?}", arr);
}
Output
100, 60, 40, 25, 50, 30, 20, 10, 15
Time Complexity of Heapify
Time Complexity of Single Heapify Operation: O(log n)
- The heapify operation (either maxHeapify or minHeapify) is applied to a single node and can involve traversing down the height of the heap to maintain the heap property.
- Since the height of a heap is O(log n) (where n is the number of elements in the heap), the time complexity of a single heapify operation is O(log n).
Time Complexity of Building a Heap: O(n)
- Even though each individual heapify call takes O(log n) time, not all nodes are at the maximum depth of the tree. In fact, many nodes are closer to the root, meaning they require fewer operations.
- The overall time complexity for building the heap can be shown to be O(n) by summing the work done at each level of the tree, using a mathematical analysis known as the heap construction analysis.
Why is Building a Heap O(n)?
- The heapify operation on the nodes closer to the bottom of the tree (which are larger in number) requires less work than the nodes closer to the root (which are fewer in number).
- Specifically, for each level of the heap, the number of nodes is halved as you move upwards, while the work required per node approximately doubles.
- Summing the work across all levels leads to a total time complexity of O(n) for building the entire heap, even though a single heapify operation is O(log n).
Now we know all the strategies to create a heap. So let's see the full implementation of Heap by using heapify method and then adding a new element to the heap and removing an element. Here I will use the recursive method of Heapify but you can replace it with the iterative implementation as needed.
Min heap
Python
class MinHeap:
def __init__(self, heap=[]) -> None:
self.heapify(heap)
self.heap = heap
def is_empty(self):
return len(self.heap) == 0
def get_max(self):
if self.is_empty():
return None
return self.heap[0]
def get_size(self):
return len(self.heap)
def get_parent_index(self, child_index):
return (child_index - 1) // 2
def get_left_child_index(self, parent_index):
return parent_index * 2 + 1
def get_right_child_index(self, parent_index):
return parent_index * 2 + 2
def __swap(self, index1, index2):
self.heap[index1], self.heap[index2] = (
self.heap[index2],
self.heap[index1],
)
def __heapify_helper(self, arr, n, i):
smallest = i
left = self.get_left_child_index(i)
right = self.get_right_child_index(i)
# If the left child is smaller than the current smallest
if left < n and arr[left] < arr[smallest]:
smallest = left
# If the right child is smaller than the current smallest
if right < n and arr[right] < arr[smallest]:
smallest = right
# If the smallest is not the root
if smallest != i:
arr[i], arr[smallest] = arr[smallest], arr[i] # Swap
self.__heapify_helper(
arr, n, smallest
) # Recursively heapify the affected subtree
def heapify(self, arr):
n = len(arr)
# Build the min heap by calling heapify for all non-leaf nodes
for i in range(n // 2 - 1, -1, -1):
self.__heapify_helper(arr, n, i)
def __percolate_up(self):
index = self.get_size() - 1
while index > 0:
parent_index = self.get_parent_index(index)
if self.heap[parent_index] > self.heap[index]:
self.__swap(parent_index, index)
index = parent_index
else:
break
def insert(self, value):
self.heap.append(value)
self.__percolate_up()
def __percolate_down(self):
parent_index = 0
while parent_index < self.get_size():
l_child_index = self.get_left_child_index(parent_index)
r_child_index = self.get_right_child_index(parent_index)
if l_child_index >= self.get_size() and r_child_index >= self.get_size():
break
new_index = -1
if r_child_index < self.get_size():
if (
self.heap[l_child_index] < self.heap[parent_index]
and self.heap[l_child_index] < self.heap[r_child_index]
):
new_index = l_child_index
elif self.heap[r_child_index] < self.heap[parent_index]:
new_index = r_child_index
elif (
self.heap[parent_index] < self.heap[l_child_index]
and self.heap[parent_index] < self.heap[r_child_index]
):
break
else:
if self.heap[l_child_index] < self.heap[parent_index]:
new_index = l_child_index
elif self.heap[parent_index] < self.heap[l_child_index]:
break
self.__swap(parent_index, new_index)
parent_index = new_index
def delete(self):
if self.is_empty():
return None
result = self.heap[0]
self.heap[0] = self.heap[self.get_size() - 1]
self.heap.pop()
self.__percolate_down()
return result
arr = [100, 60, 40, 30, 50, 15, 20, 10, 25]
min_heap = MinHeap(arr)
print(min_heap.delete())
print(min_heap.delete())
print(min_heap.delete())
min_heap.insert(10)
print(min_heap.delete())
JavaScript
class MinHeap {
constructor(heap = []) {
this.heap = heap;
this.heapify(heap);
}
isEmpty() {
return this.heap.length === 0;
}
getMax() {
if (this.isEmpty()) {
return null;
}
return this.heap[0];
}
getSize() {
return this.heap.length;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
getLeftChildIndex(parentIndex) {
return parentIndex * 2 + 1;
}
getRightChildIndex(parentIndex) {
return parentIndex * 2 + 2;
}
swap(index1, index2) {
[this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
}
heapifyHelper(arr, n, i) {
let smallest = i;
let left = this.getLeftChildIndex(i);
let right = this.getRightChildIndex(i);
// If the left child is smaller than the current smallest
if (left < n && arr[left] < arr[smallest]) {
smallest = left;
}
// If the right child is smaller than the current smallest
if (right < n && arr[right] < arr[smallest]) {
smallest = right;
}
// If the smallest is not the root
if (smallest !== i) {
[arr[i], arr[smallest]] = [arr[smallest], arr[i]]; // Swap
this.heapifyHelper(arr, n, smallest); // Recursively heapify the affected subtree
}
}
heapify(arr) {
const n = arr.length;
// Build the min heap by calling heapify for all non-leaf nodes
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
this.heapifyHelper(arr, n, i);
}
}
percolateUp() {
let index = this.getSize() - 1;
while (index > 0) {
const parentIndex = this.getParentIndex(index);
if (this.heap[parentIndex] > this.heap[index]) {
this.swap(parentIndex, index);
index = parentIndex;
} else {
break;
}
}
}
insert(value) {
this.heap.push(value);
this.percolateUp();
}
percolateDown() {
let parentIndex = 0;
while (parentIndex < this.getSize()) {
const lChildIndex = this.getLeftChildIndex(parentIndex);
const rChildIndex = this.getRightChildIndex(parentIndex);
if (lChildIndex >= this.getSize() && rChildIndex >= this.getSize()) {
break;
}
let newIndex = -1;
if (rChildIndex < this.getSize()) {
if (this.heap[lChildIndex] < this.heap[parentIndex] && this.heap[lChildIndex] < this.heap[rChildIndex]) {
newIndex = lChildIndex;
} else if (this.heap[rChildIndex] < this.heap[parentIndex]) {
newIndex = rChildIndex;
} else if (this.heap[parentIndex] < this.heap[lChildIndex] && this.heap[parentIndex] < this.heap[rChildIndex]) {
break;
}
} else {
if (this.heap[lChildIndex] < this.heap[parentIndex]) {
newIndex = lChildIndex;
} else if (this.heap[parentIndex] < this.heap[lChildIndex]) {
break;
}
}
this.swap(parentIndex, newIndex);
parentIndex = newIndex;
}
}
delete() {
if (this.isEmpty()) {
return null;
}
const result = this.heap[0];
this.heap[0] = this.heap[this.getSize() - 1];
this.heap.pop();
this.percolateDown();
return result;
}
}
const arr = [100, 60, 40, 30, 50, 15, 20, 10, 25];
const minHeap = new MinHeap(arr);
console.log(minHeap.delete());
console.log(minHeap.delete());
console.log(minHeap.delete());
minHeap.insert(10);
console.log(minHeap.delete());
Java
import java.util.ArrayList;
import java.util.List;
public class MinHeap {
private List<Integer> heap;
public MinHeap(List<Integer> heap) {
this.heap = heap;
heapify();
}
public boolean isEmpty() {
return heap.isEmpty();
}
public int getMin() {
if (isEmpty()) {
return -1; // Return a sentinel value or throw an exception as needed
}
return heap.get(0);
}
public int getSize() {
return heap.size();
}
private int getParentIndex(int childIndex) {
return (childIndex - 1) / 2;
}
private int getLeftChildIndex(int parentIndex) {
return 2 * parentIndex + 1;
}
private int getRightChildIndex(int parentIndex) {
return 2 * parentIndex + 2;
}
private void swap(int index1, int index2) {
int temp = heap.get(index1);
heap.set(index1, heap.get(index2));
heap.set(index2, temp);
}
private void heapifyHelper(int n, int i) {
int smallest = i;
int left = getLeftChildIndex(i);
int right = getRightChildIndex(i);
if (left < n && heap.get(left) < heap.get(smallest)) {
smallest = left;
}
if (right < n && heap.get(right) < heap.get(smallest)) {
smallest = right;
}
if (smallest != i) {
swap(i, smallest);
heapifyHelper(n, smallest);
}
}
private void heapify() {
int n = heap.size();
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(n, i);
}
}
private void percolateUp() {
int index = getSize() - 1;
while (index > 0) {
int parentIndex = getParentIndex(index);
if (heap.get(parentIndex) > heap.get(index)) {
swap(parentIndex, index);
index = parentIndex;
} else {
break;
}
}
}
public void insert(int value) {
heap.add(value);
percolateUp();
}
private void percolateDown() {
int parentIndex = 0;
int size = getSize();
while (parentIndex < size) {
int lChildIndex = getLeftChildIndex(parentIndex);
int rChildIndex = getRightChildIndex(parentIndex);
if (lChildIndex >= size && rChildIndex >= size) {
break;
}
int newIndex = -1;
if (rChildIndex < size) {
if (heap.get(lChildIndex) < heap.get(parentIndex) && heap.get(lChildIndex) < heap.get(rChildIndex)) {
newIndex = lChildIndex;
} else if (heap.get(rChildIndex) < heap.get(parentIndex)) {
newIndex = rChildIndex;
} else if (heap.get(parentIndex) < heap.get(lChildIndex) && heap.get(parentIndex) < heap.get(rChildIndex)) {
break;
}
} else {
if (heap.get(lChildIndex) < heap.get(parentIndex)) {
newIndex = lChildIndex;
} else if (heap.get(parentIndex) < heap.get(lChildIndex)) {
break;
}
}
swap(parentIndex, newIndex);
parentIndex = newIndex;
}
}
public int delete() {
if (isEmpty()) {
return -1; // Return a sentinel value or throw an exception as needed
}
int result = heap.get(0);
heap.set(0, heap.get(getSize() - 1));
heap.remove(getSize() - 1);
percolateDown();
return result;
}
public static void main(String[] args) {
List<Integer> arr = new ArrayList<>(List.of(100, 60, 40, 30, 50, 15, 20, 10, 25));
MinHeap minHeap = new MinHeap(arr);
System.out.println(minHeap.delete());
System.out.println(minHeap.delete());
System.out.println(minHeap.delete());
minHeap.insert(10);
System.out.println(minHeap.delete());
}
}
Go
package main
import (
"fmt"
)
type MinHeap struct {
heap []int
}
// NewMinHeap initializes a new MinHeap and heapifies the provided array.
func NewMinHeap(arr []int) *MinHeap {
mh := &MinHeap{heap: arr}
mh.heapify()
return mh
}
// isEmpty checks if the heap is empty.
func (mh *MinHeap) isEmpty() bool {
return len(mh.heap) == 0
}
// getMin returns the minimum element from the heap.
func (mh *MinHeap) getMin() int {
if mh.isEmpty() {
return -1 // or some other sentinel value
}
return mh.heap[0]
}
// getSize returns the size of the heap.
func (mh *MinHeap) getSize() int {
return len(mh.heap)
}
// getParentIndex returns the index of the parent of a given child index.
func (mh *MinHeap) getParentIndex(childIndex int) int {
return (childIndex - 1) / 2
}
// getLeftChildIndex returns the index of the left child of a given parent index.
func (mh *MinHeap) getLeftChildIndex(parentIndex int) int {
return 2*parentIndex + 1
}
// getRightChildIndex returns the index of the right child of a given parent index.
func (mh *MinHeap) getRightChildIndex(parentIndex int) int {
return 2*parentIndex + 2
}
// swap exchanges the elements at two given indices.
func (mh *MinHeap) swap(index1, index2 int) {
mh.heap[index1], mh.heap[index2] = mh.heap[index2], mh.heap[index1]
}
// heapifyHelper helps maintain the min-heap property.
func (mh *MinHeap) heapifyHelper(n, i int) {
smallest := i
left := mh.getLeftChildIndex(i)
right := mh.getRightChildIndex(i)
if left < n && mh.heap[left] < mh.heap[smallest] {
smallest = left
}
if right < n && mh.heap[right] < mh.heap[smallest] {
smallest = right
}
if smallest != i {
mh.swap(i, smallest)
mh.heapifyHelper(n, smallest)
}
}
// heapify builds the min-heap from the array.
func (mh *MinHeap) heapify() {
n := len(mh.heap)
for i := n/2 - 1; i >= 0; i-- {
mh.heapifyHelper(n, i)
}
}
// percolateUp moves a newly added element up to maintain the min-heap property.
func (mh *MinHeap) percolateUp() {
index := mh.getSize() - 1
for index > 0 {
parentIndex := mh.getParentIndex(index)
if mh.heap[parentIndex] > mh.heap[index] {
mh.swap(parentIndex, index)
index = parentIndex
} else {
break
}
}
}
// Insert adds a new element to the heap.
func (mh *MinHeap) Insert(value int) {
mh.heap = append(mh.heap, value)
mh.percolateUp()
}
// percolateDown moves an element down to maintain the min-heap property.
func (mh *MinHeap) percolateDown() {
parentIndex := 0
size := mh.getSize()
for {
leftChildIndex := mh.getLeftChildIndex(parentIndex)
rightChildIndex := mh.getRightChildIndex(parentIndex)
if leftChildIndex >= size && rightChildIndex >= size {
break
}
newIndex := -1
if rightChildIndex < size {
if mh.heap[leftChildIndex] < mh.heap[parentIndex] && mh.heap[leftChildIndex] < mh.heap[rightChildIndex] {
newIndex = leftChildIndex
} else if mh.heap[rightChildIndex] < mh.heap[parentIndex] {
newIndex = rightChildIndex
} else if mh.heap[parentIndex] < mh.heap[leftChildIndex] && mh.heap[parentIndex] < mh.heap[rightChildIndex] {
break
}
} else {
if mh.heap[leftChildIndex] < mh.heap[parentIndex] {
newIndex = leftChildIndex
} else if mh.heap[parentIndex] < mh.heap[leftChildIndex] {
break
}
}
if newIndex != -1 {
mh.swap(parentIndex, newIndex)
parentIndex = newIndex
} else {
break
}
}
}
// Delete removes and returns the minimum element from the heap.
func (mh *MinHeap) Delete() int {
if mh.isEmpty() {
return -1 // or some other sentinel value
}
result := mh.heap[0]
mh.heap[0] = mh.heap[mh.getSize()-1]
mh.heap = mh.heap[:mh.getSize()-1]
mh.percolateDown()
return result
}
func main() {
arr := []int{100, 60, 40, 30, 50, 15, 20, 10, 25}
minHeap := NewMinHeap(arr)
fmt.Println(minHeap.Delete())
fmt.Println(minHeap.Delete())
fmt.Println(minHeap.Delete())
minHeap.Insert(10)
fmt.Println(minHeap.Delete())
}
C++
#include <iostream>
#include <vector>
class MinHeap {
private:
std::vector<int> heap;
int getParentIndex(int childIndex) {
return (childIndex - 1) / 2;
}
int getLeftChildIndex(int parentIndex) {
return parentIndex * 2 + 1;
}
int getRightChildIndex(int parentIndex) {
return parentIndex * 2 + 2;
}
void swap(int index1, int index2) {
std::swap(heap[index1], heap[index2]);
}
void heapifyHelper(std::vector<int>& arr, int n, int i) {
int smallest = i;
int left = getLeftChildIndex(i);
int right = getRightChildIndex(i);
if (left < n && arr[left] < arr[smallest])
smallest = left;
if (right < n && arr[right] < arr[smallest])
smallest = right;
if (smallest != i) {
std::swap(arr[i], arr[smallest]);
heapifyHelper(arr, n, smallest);
}
}
void heapify() {
int n = heap.size();
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(heap, n, i);
}
}
void percolateUp() {
int index = heap.size() - 1;
while (index > 0) {
int parentIndex = getParentIndex(index);
if (heap[parentIndex] > heap[index]) {
swap(parentIndex, index);
index = parentIndex;
} else {
break;
}
}
}
void percolateDown() {
int parentIndex = 0;
while (parentIndex < heap.size()) {
int l_child_index = getLeftChildIndex(parentIndex);
int r_child_index = getRightChildIndex(parentIndex);
if (l_child_index >= heap.size() && r_child_index >= heap.size())
break;
int new_index = -1;
if (r_child_index < heap.size()) {
if (heap[l_child_index] < heap[parentIndex] &&
heap[l_child_index] < heap[r_child_index]) {
new_index = l_child_index;
} else if (heap[r_child_index] < heap[parentIndex]) {
new_index = r_child_index;
} else if (heap[parentIndex] < heap[l_child_index] &&
heap[parentIndex] < heap[r_child_index]) {
break;
}
} else {
if (heap[l_child_index] < heap[parentIndex]) {
new_index = l_child_index;
} else if (heap[parentIndex] < heap[l_child_index]) {
break;
}
}
if (new_index != -1) {
swap(parentIndex, new_index);
parentIndex = new_index;
} else {
break;
}
}
}
public:
MinHeap(std::vector<int> arr) : heap(arr) {
heapify();
}
bool isEmpty() const {
return heap.empty();
}
int getMin() const {
if (isEmpty())
return -1;
return heap[0];
}
int getSize() const {
return heap.size();
}
void insert(int value) {
heap.push_back(value);
percolateUp();
}
int deleteMin() {
if (isEmpty())
return -1;
int result = heap[0];
heap[0] = heap.back();
heap.pop_back();
percolateDown();
return result;
}
};
int main() {
std::vector<int> arr = {100, 60, 40, 30, 50, 15, 20, 10, 25};
MinHeap minHeap(arr);
std::cout << minHeap.deleteMin() << std::endl;
std::cout << minHeap.deleteMin() << std::endl;
std::cout << minHeap.deleteMin() << std::endl;
minHeap.insert(10);
std::cout << minHeap.deleteMin() << std::endl;
return 0;
}
Rust
struct MinHeap {
heap: Vec<i32>,
}
impl MinHeap {
// Initialize the heap and heapify the input array
fn new(mut heap: Vec<i32>) -> Self {
let n = heap.len();
for i in (0..n / 2).rev() {
Self::heapify_helper(&mut heap, n, i);
}
MinHeap { heap }
}
// Check if the heap is empty
fn is_empty(&self) -> bool {
self.heap.is_empty()
}
// Get the minimum element (root) of the heap
fn get_min(&self) -> Option<i32> {
if self.is_empty() {
None
} else {
Some(self.heap[0])
}
}
// Get the size of the heap
fn get_size(&self) -> usize {
self.heap.len()
}
// Get the parent index of a given child index
fn get_parent_index(child_index: usize) -> usize {
(child_index - 1) / 2
}
// Get the left child index of a given parent index
fn get_left_child_index(parent_index: usize) -> usize {
2 * parent_index + 1
}
// Get the right child index of a given parent index
fn get_right_child_index(parent_index: usize) -> usize {
2 * parent_index + 2
}
// Swap two elements in the heap
fn swap(heap: &mut Vec<i32>, index1: usize, index2: usize) {
heap.swap(index1, index2);
}
// Heapify the subtree rooted at index `i`
fn heapify_helper(heap: &mut Vec<i32>, n: usize, i: usize) {
let mut smallest = i;
let left = Self::get_left_child_index(i);
let right = Self::get_right_child_index(i);
if left < n && heap[left] < heap[smallest] {
smallest = left;
}
if right < n && heap[right] < heap[smallest] {
smallest = right;
}
if smallest != i {
Self::swap(heap, i, smallest);
Self::heapify_helper(heap, n, smallest);
}
}
// Percolate up to maintain the heap property after insertion
fn percolate_up(&mut self) {
let mut index = self.get_size() - 1;
while index > 0 {
let parent_index = Self::get_parent_index(index);
if self.heap[parent_index] > self.heap[index] {
Self::swap(&mut self.heap, parent_index, index);
index = parent_index;
} else {
break;
}
}
}
// Insert a new value into the heap
fn insert(&mut self, value: i32) {
self.heap.push(value);
self.percolate_up();
}
// Percolate down to maintain the heap property after deletion
fn percolate_down(&mut self) {
let mut parent_index = 0;
let size = self.get_size();
loop {
let l_child_index = Self::get_left_child_index(parent_index);
let r_child_index = Self::get_right_child_index(parent_index);
let mut new_index = None;
if l_child_index >= size && r_child_index >= size {
break;
}
if r_child_index < size {
if self.heap[l_child_index] < self.heap[parent_index]
&& self.heap[l_child_index] < self.heap[r_child_index]
{
new_index = Some(l_child_index);
} else if self.heap[r_child_index] < self.heap[parent_index] {
new_index = Some(r_child_index);
}
} else if self.heap[l_child_index] < self.heap[parent_index] {
new_index = Some(l_child_index);
}
if let Some(new_index) = new_index {
Self::swap(&mut self.heap, parent_index, new_index);
parent_index = new_index;
} else {
break;
}
}
}
// Remove and return the minimum element (root) of the heap
fn delete_min(&mut self) -> Option<i32> {
if self.is_empty() {
return None;
}
let result = self.heap[0];
let last = self.heap.pop().unwrap();
if !self.is_empty() {
self.heap[0] = last;
self.percolate_down();
}
Some(result)
}
}
fn main() {
let arr = vec![100, 60, 40, 30, 50, 15, 20, 10, 25];
let mut min_heap = MinHeap::new(arr);
println!("{:?}", min_heap.delete_min());
println!("{:?}", min_heap.delete_min());
println!("{:?}", min_heap.delete_min());
min_heap.insert(10);
println!("{:?}", min_heap.delete_min());
}
Output
10
15
20
10
Max heap
Python
class MaxHeap:
def __init__(self, heap=[]) -> None:
self.heapify(heap)
self.heap = heap
def is_empty(self):
return len(self.heap) == 0
def get_max(self):
if self.is_empty():
return None
return self.heap[0]
def get_size(self):
return len(self.heap)
def get_parent_index(self, child_index):
return (child_index - 1) // 2
def get_left_child_index(self, parent_index):
return parent_index * 2 + 1
def get_right_child_index(self, parent_index):
return parent_index * 2 + 2
def __swap(self, index1, index2):
self.heap[index1], self.heap[index2] = (
self.heap[index2],
self.heap[index1],
)
def __heapify_helper(self, arr, n, i):
largest = i # Initialize the largest as the root
left = 2 * i + 1 # Left child
right = 2 * i + 2 # Right child
# If the left child exists and is greater than the root
if left < n and arr[left] > arr[largest]:
largest = left
# If the right child exists and is greater than the current largest
if right < n and arr[right] > arr[largest]:
largest = right
# If the largest is not the root, swap and continue heapifying
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # Swap
self.__heapify_helper(
arr, n, largest
) # Recursively heapify the affected subtree
def heapify(self, arr):
n = len(arr)
# Build the max heap by calling heapify for all non-leaf nodes
for i in range(n // 2 - 1, -1, -1):
self.__heapify_helper(arr, n, i)
def __percolate_up(self):
index = self.get_size() - 1
while index > 0:
parent_index = self.get_parent_index(index)
if self.heap[index] > self.heap[parent_index]:
self.__swap(index, parent_index)
index = parent_index
else:
break
def insert(self, value):
self.heap.append(value)
self.__percolate_up()
def __percolate_down(self):
parent_index = 0
left_child_index = self.get_left_child_index(parent_index)
right_child_index = self.get_right_child_index(parent_index)
while left_child_index < self.get_size():
max_index = parent_index
if self.heap[left_child_index] > self.heap[max_index]:
max_index = left_child_index
if (
right_child_index < self.get_size()
and self.heap[right_child_index] > self.heap[max_index]
):
max_index = right_child_index
if max_index == parent_index:
break
self.__swap(max_index, parent_index)
parent_index = max_index
left_child_index = self.get_left_child_index(parent_index)
right_child_index = self.get_right_child_index(parent_index)
def delete(self):
if self.is_empty():
return None
result = self.heap[0]
self.heap[0] = self.heap[self.get_size() - 1]
self.heap.pop()
self.__percolate_down()
return result
arr = [25, 10, 20, 15, 50, 30, 40, 60, 100]
max_heap = MaxHeap(arr)
print(max_heap.delete())
print(max_heap.delete())
print(max_heap.delete())
max_heap.insert(60)
print(max_heap.delete())
JavaScript
class MaxHeap {
constructor(heap = []) {
this.heapify(heap);
this.heap = heap;
}
isEmpty() {
return this.heap.length === 0;
}
getMax() {
if (this.isEmpty()) {
return null;
}
return this.heap[0];
}
getSize() {
return this.heap.length;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
getLeftChildIndex(parentIndex) {
return parentIndex * 2 + 1;
}
getRightChildIndex(parentIndex) {
return parentIndex * 2 + 2;
}
swap(index1, index2) {
[this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
}
heapifyHelper(arr, n, i) {
let largest = i; // Initialize largest as root
let left = 2 * i + 1; // Left child
let right = 2 * i + 2; // Right child
// If the left child exists and is greater than the root
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// If the right child exists and is greater than the current largest
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// If the largest is not the root, swap and continue heapifying
if (largest !== i) {
[arr[i], arr[largest]] = [arr[largest], arr[i]]; // Swap
this.heapifyHelper(arr, n, largest); // Recursively heapify the affected subtree
}
}
heapify(arr) {
const n = arr.length;
// Build the max heap by calling heapify for all non-leaf nodes
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
this.heapifyHelper(arr, n, i);
}
}
percolateUp() {
let index = this.getSize() - 1;
while (index > 0) {
const parentIndex = this.getParentIndex(index);
if (this.heap[index] > this.heap[parentIndex]) {
this.swap(index, parentIndex);
index = parentIndex;
} else {
break;
}
}
}
insert(value) {
this.heap.push(value);
this.percolateUp();
}
percolateDown() {
let parentIndex = 0;
let leftChildIndex = this.getLeftChildIndex(parentIndex);
let rightChildIndex = this.getRightChildIndex(parentIndex);
while (leftChildIndex < this.getSize()) {
let maxIndex = parentIndex;
if (this.heap[leftChildIndex] > this.heap[maxIndex]) {
maxIndex = leftChildIndex;
}
if (rightChildIndex < this.getSize() && this.heap[rightChildIndex] > this.heap[maxIndex]) {
maxIndex = rightChildIndex;
}
if (maxIndex === parentIndex) {
break;
}
this.swap(maxIndex, parentIndex);
parentIndex = maxIndex;
leftChildIndex = this.getLeftChildIndex(parentIndex);
rightChildIndex = this.getRightChildIndex(parentIndex);
}
}
delete() {
if (this.isEmpty()) {
return null;
}
const result = this.heap[0];
this.heap[0] = this.heap.pop();
this.percolateDown();
return result;
}
}
const arr = [25, 10, 20, 15, 50, 30, 40, 60, 100];
const maxHeap = new MaxHeap(arr);
console.log(maxHeap.delete());
console.log(maxHeap.delete());
console.log(maxHeap.delete());
maxHeap.insert(60);
console.log(maxHeap.delete());
Java
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
private List<Integer> heap;
public MaxHeap(List<Integer> heap) {
this.heap = heap;
heapify(this.heap);
}
public boolean isEmpty() {
return heap.isEmpty();
}
public Integer getMax() {
if (isEmpty()) {
return null;
}
return heap.get(0);
}
public int getSize() {
return heap.size();
}
public int getParentIndex(int childIndex) {
return (childIndex - 1) / 2;
}
public int getLeftChildIndex(int parentIndex) {
return parentIndex * 2 + 1;
}
public int getRightChildIndex(int parentIndex) {
return parentIndex * 2 + 2;
}
private void swap(int index1, int index2) {
int temp = heap.get(index1);
heap.set(index1, heap.get(index2));
heap.set(index2, temp);
}
private void heapifyHelper(List<Integer> arr, int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr.get(left) > arr.get(largest)) {
largest = left;
}
if (right < n && arr.get(right) > arr.get(largest)) {
largest = right;
}
if (largest != i) {
swap(i, largest);
heapifyHelper(arr, n, largest);
}
}
public void heapify(List<Integer> arr) {
int n = arr.size();
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(arr, n, i);
}
}
private void percolateUp() {
int index = getSize() - 1;
while (index > 0) {
int parentIndex = getParentIndex(index);
if (heap.get(index) > heap.get(parentIndex)) {
swap(index, parentIndex);
index = parentIndex;
} else {
break;
}
}
}
public void insert(int value) {
heap.add(value);
percolateUp();
}
private void percolateDown() {
int parentIndex = 0;
int leftChildIndex = getLeftChildIndex(parentIndex);
int rightChildIndex = getRightChildIndex(parentIndex);
while (leftChildIndex < getSize()) {
int maxIndex = parentIndex;
if (heap.get(leftChildIndex) > heap.get(maxIndex)) {
maxIndex = leftChildIndex;
}
if (rightChildIndex < getSize() && heap.get(rightChildIndex) > heap.get(maxIndex)) {
maxIndex = rightChildIndex;
}
if (maxIndex == parentIndex) {
break;
}
swap(maxIndex, parentIndex);
parentIndex = maxIndex;
leftChildIndex = getLeftChildIndex(parentIndex);
rightChildIndex = getRightChildIndex(parentIndex);
}
}
public Integer delete() {
if (isEmpty()) {
return null;
}
int result = heap.get(0);
heap.set(0, heap.get(getSize() - 1));
heap.remove(getSize() - 1);
percolateDown();
return result;
}
public static void main(String[] args) {
List<Integer> arr = new ArrayList<>();
arr.add(25);
arr.add(10);
arr.add(20);
arr.add(15);
arr.add(50);
arr.add(30);
arr.add(40);
arr.add(60);
arr.add(100);
MaxHeap maxHeap = new MaxHeap(arr);
System.out.println(maxHeap.delete());
System.out.println(maxHeap.delete());
System.out.println(maxHeap.delete());
maxHeap.insert(60);
System.out.println(maxHeap.delete());
}
}
Go
package main
import (
"fmt"
)
type MaxHeap struct {
heap []int
}
func NewMaxHeap(arr []int) *MaxHeap {
h := &MaxHeap{heap: arr}
h.heapify()
return h
}
func (h *MaxHeap) isEmpty() bool {
return len(h.heap) == 0
}
func (h *MaxHeap) getMax() *int {
if h.isEmpty() {
return nil
}
return &h.heap[0]
}
func (h *MaxHeap) getSize() int {
return len(h.heap)
}
func (h *MaxHeap) getParentIndex(childIndex int) int {
return (childIndex - 1) / 2
}
func (h *MaxHeap) getLeftChildIndex(parentIndex int) int {
return 2*parentIndex + 1
}
func (h *MaxHeap) getRightChildIndex(parentIndex int) int {
return 2*parentIndex + 2
}
func (h *MaxHeap) swap(index1, index2 int) {
h.heap[index1], h.heap[index2] = h.heap[index2], h.heap[index1]
}
func (h *MaxHeap) heapifyHelper(n, i int) {
largest := i
left := 2*i + 1
right := 2*i + 2
if left < n && h.heap[left] > h.heap[largest] {
largest = left
}
if right < n && h.heap[right] > h.heap[largest] {
largest = right
}
if largest != i {
h.swap(i, largest)
h.heapifyHelper(n, largest)
}
}
func (h *MaxHeap) heapify() {
n := len(h.heap)
for i := n/2 - 1; i >= 0; i-- {
h.heapifyHelper(n, i)
}
}
func (h *MaxHeap) percolateUp() {
index := h.getSize() - 1
for index > 0 {
parentIndex := h.getParentIndex(index)
if h.heap[index] > h.heap[parentIndex] {
h.swap(index, parentIndex)
index = parentIndex
} else {
break
}
}
}
func (h *MaxHeap) insert(value int) {
h.heap = append(h.heap, value)
h.percolateUp()
}
func (h *MaxHeap) percolateDown() {
parentIndex := 0
for {
leftChildIndex := h.getLeftChildIndex(parentIndex)
rightChildIndex := h.getRightChildIndex(parentIndex)
if leftChildIndex >= h.getSize() {
break
}
maxIndex := parentIndex
if h.heap[leftChildIndex] > h.heap[maxIndex] {
maxIndex = leftChildIndex
}
if rightChildIndex < h.getSize() && h.heap[rightChildIndex] > h.heap[maxIndex] {
maxIndex = rightChildIndex
}
if maxIndex == parentIndex {
break
}
h.swap(parentIndex, maxIndex)
parentIndex = maxIndex
}
}
func (h *MaxHeap) delete() *int {
if h.isEmpty() {
return nil
}
result := h.heap[0]
h.heap[0] = h.heap[h.getSize()-1]
h.heap = h.heap[:h.getSize()-1]
h.percolateDown()
return &result
}
func main() {
arr := []int{25, 10, 20, 15, 50, 30, 40, 60, 100}
maxHeap := NewMaxHeap(arr)
fmt.Println(*maxHeap.delete())
fmt.Println(*maxHeap.delete())
fmt.Println(*maxHeap.delete())
maxHeap.insert(60)
fmt.Println(*maxHeap.delete())
}
C++
#include <iostream>
#include <vector>
class MaxHeap {
public:
MaxHeap(std::vector<int>& arr) : heap(arr) {
heapify();
}
bool isEmpty() const {
return heap.empty();
}
int getMax() const {
if (isEmpty()) {
throw std::runtime_error("Heap is empty");
}
return heap[0];
}
size_t getSize() const {
return heap.size();
}
void insert(int value) {
heap.push_back(value);
percolateUp();
}
int deleteMax() {
if (isEmpty()) {
throw std::runtime_error("Heap is empty");
}
int result = heap[0];
heap[0] = heap[getSize() - 1];
heap.pop_back();
percolateDown();
return result;
}
private:
std::vector<int> heap;
int getParentIndex(int childIndex) const {
return (childIndex - 1) / 2;
}
int getLeftChildIndex(int parentIndex) const {
return 2 * parentIndex + 1;
}
int getRightChildIndex(int parentIndex) const {
return 2 * parentIndex + 2;
}
void swap(int index1, int index2) {
std::swap(heap[index1], heap[index2]);
}
void heapifyHelper(int n, int i) {
int largest = i;
int left = getLeftChildIndex(i);
int right = getRightChildIndex(i);
if (left < n && heap[left] > heap[largest]) {
largest = left;
}
if (right < n && heap[right] > heap[largest]) {
largest = right;
}
if (largest != i) {
swap(i, largest);
heapifyHelper(n, largest);
}
}
void heapify() {
int n = heap.size();
for (int i = n / 2 - 1; i >= 0; i--) {
heapifyHelper(n, i);
}
}
void percolateUp() {
int index = getSize() - 1;
while (index > 0) {
int parentIndex = getParentIndex(index);
if (heap[index] > heap[parentIndex]) {
swap(index, parentIndex);
index = parentIndex;
} else {
break;
}
}
}
void percolateDown() {
int parentIndex = 0;
while (true) {
int leftChildIndex = getLeftChildIndex(parentIndex);
int rightChildIndex = getRightChildIndex(parentIndex);
if (leftChildIndex >= getSize()) {
break;
}
int maxIndex = parentIndex;
if (heap[leftChildIndex] > heap[maxIndex]) {
maxIndex = leftChildIndex;
}
if (rightChildIndex < getSize() && heap[rightChildIndex] > heap[maxIndex]) {
maxIndex = rightChildIndex;
}
if (maxIndex == parentIndex) {
break;
}
swap(parentIndex, maxIndex);
parentIndex = maxIndex;
}
}
};
int main() {
std::vector<int> arr = {25, 10, 20, 15, 50, 30, 40, 60, 100};
MaxHeap maxHeap(arr);
std::cout << maxHeap.deleteMax() << std::endl;
std::cout << maxHeap.deleteMax() << std::endl;
std::cout << maxHeap.deleteMax() << std::endl;
maxHeap.insert(60);
std::cout << maxHeap.deleteMax() << std::endl;
return 0;
}
Rust
struct MaxHeap {
heap: Vec<i32>,
}
impl MaxHeap {
fn new(mut arr: Vec<i32>) -> Self {
let mut heap = MaxHeap { heap: arr };
heap.heapify();
heap
}
fn is_empty(&self) -> bool {
self.heap.is_empty()
}
fn get_max(&self) -> Option<i32> {
if self.is_empty() {
None
} else {
Some(self.heap[0])
}
}
fn get_size(&self) -> usize {
self.heap.len()
}
fn get_parent_index(&self, child_index: usize) -> usize {
(child_index - 1) / 2
}
fn get_left_child_index(&self, parent_index: usize) -> usize {
2 * parent_index + 1
}
fn get_right_child_index(&self, parent_index: usize) -> usize {
2 * parent_index + 2
}
fn swap(&mut self, index1: usize, index2: usize) {
self.heap.swap(index1, index2);
}
fn heapify_helper(&mut self, n: usize, i: usize) {
let mut largest = i;
let left = self.get_left_child_index(i);
let right = self.get_right_child_index(i);
if left < n && self.heap[left] > self.heap[largest] {
largest = left;
}
if right < n && self.heap[right] > self.heap[largest] {
largest = right;
}
if largest != i {
self.swap(i, largest);
self.heapify_helper(n, largest);
}
}
fn heapify(&mut self) {
let n = self.heap.len();
for i in (0..n / 2).rev() {
self.heapify_helper(n, i);
}
}
fn percolate_up(&mut self) {
let mut index = self.get_size() - 1;
while index > 0 {
let parent_index = self.get_parent_index(index);
if self.heap[index] > self.heap[parent_index] {
self.swap(index, parent_index);
index = parent_index;
} else {
break;
}
}
}
fn insert(&mut self, value: i32) {
self.heap.push(value);
self.percolate_up();
}
fn percolate_down(&mut self) {
let mut parent_index = 0;
while let Some(left_child_index) = self.get_left_child_index_checked(parent_index) {
let right_child_index = self.get_right_child_index_checked(parent_index);
let mut max_index = parent_index;
if self.heap[left_child_index] > self.heap[max_index] {
max_index = left_child_index;
}
if let Some(right_index) = right_child_index {
if self.heap[right_index] > self.heap[max_index] {
max_index = right_index;
}
}
if max_index == parent_index {
break;
}
self.swap(parent_index, max_index);
parent_index = max_index;
}
}
fn get_left_child_index_checked(&self, parent_index: usize) -> Option<usize> {
let index = self.get_left_child_index(parent_index);
if index < self.get_size() {
Some(index)
} else {
None
}
}
fn get_right_child_index_checked(&self, parent_index: usize) -> Option<usize> {
let index = self.get_right_child_index(parent_index);
if index < self.get_size() {
Some(index)
} else {
None
}
}
fn delete(&mut self) -> Option<i32> {
if self.is_empty() {
return None;
}
let result = self.heap[0];
let last = self.heap.pop()?;
if !self.heap.is_empty() {
self.heap[0] = last;
self.percolate_down();
}
Some(result)
}
}
fn main() {
let arr = vec![25, 10, 20, 15, 50, 30, 40, 60, 100];
let mut max_heap = MaxHeap::new(arr);
println!("{:?}", max_heap.delete());
println!("{:?}", max_heap.delete());
println!("{:?}", max_heap.delete());
max_heap.insert(60);
println!("{:?}", max_heap.delete());
}
Output
100
60
50
60
Application of heapify
- Heap Sort: Heapify is a critical step in the heap sort algorithm, which sorts an array by first converting it into a heap and then repeatedly removing the root (the minimum or maximum element) and re-heapifying the remaining elements.
- Priority Queues: Heapify is used to maintain the heap property in priority queues, allowing for efficient access to the highest or lowest priority element.