Introduction to Binary Tree

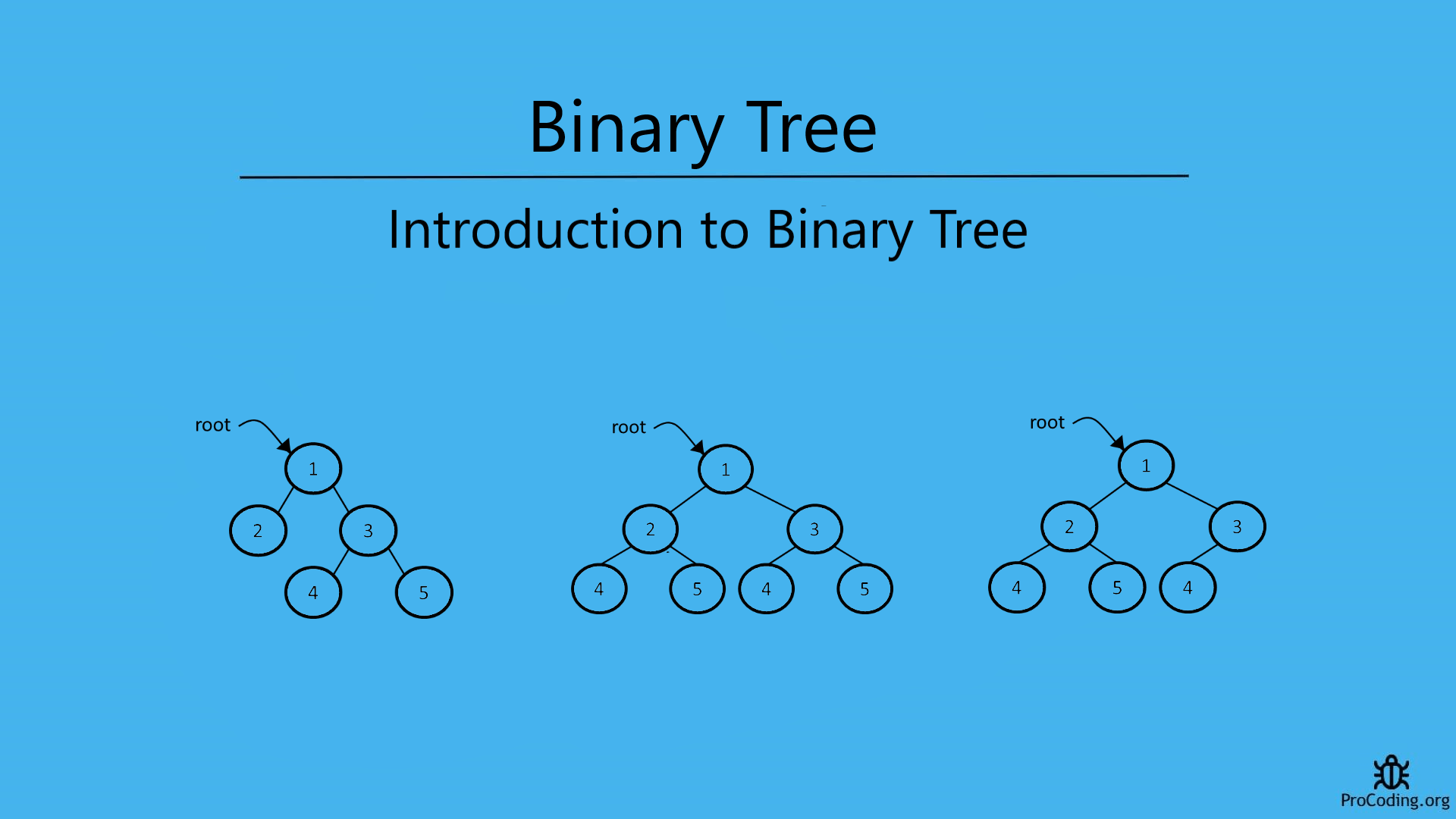
Table of contents

• Types of binary trees
• Properties of a Binary Trees
• Structure of a Binary Tree
• Operations on a Binary Tree
• Insertion in a Binary Tree
  1. Insertion at left
  2. Insertion at right

A binary tree is a non-linear and hierarchical data structure which has zero child, one child or two children. Empty tree is also a valid binary tree. Each node has three parts i.e., data, pointer to left child node and pointer to right node.

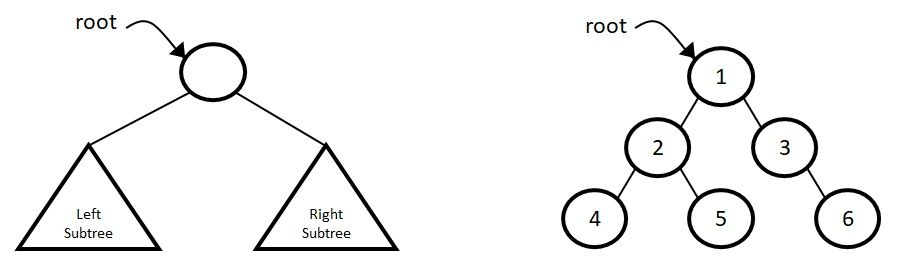
Types of binary trees

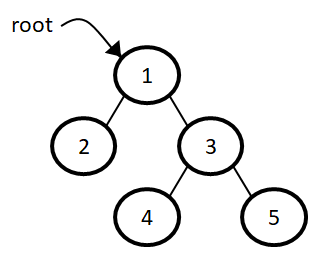
Strict binary tree: A binary tree is called strict binary tree if each node has either two children or no children.

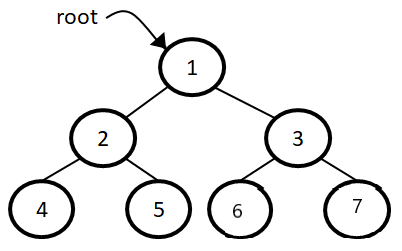
Full binary tree: A binary tree is called full binary tree if each node has exactly two children and all leaf nodes have no children.

Complete binary tree: A binary tree is called a complete binary tree if all the levels are completely filled except the lowest one which is filled from left.

When we try to create a full binary tree and insertion is done from the left most node and from the top level by filling each level completely but still is there are some nodes to required by it to become a full binary tree. That intermediate state can be called as complete binary tree.

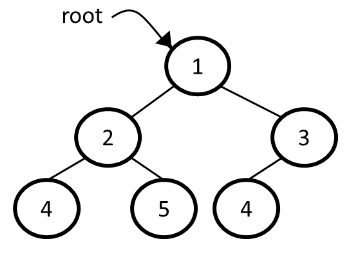
Properties of a Binary Trees

• The number of nodes(n) in a full binary tree is 2^(h+1).
• The number of leaf node in a full binary tree is 2^h.
• A binary tree of n nodes has (n+1) null references.
• The minimum and the maximum height of a binary tree having n nodes are ⌈log2n⌉ and n, respectively.

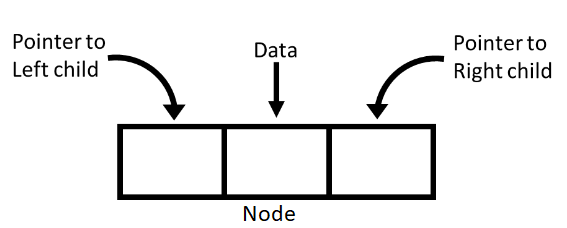
Structure of a Binary Tree

In a binary tree, each node has three part i.e., data, pointer to left child and pointer to right child.

class Node:
    def __init__(self, data):
        self.left = None
        self.data = data
        self.right = None

class Node {
  constructor(data) {
    this.left = null;
    this.data = data;
    this.right = null;
  }
}

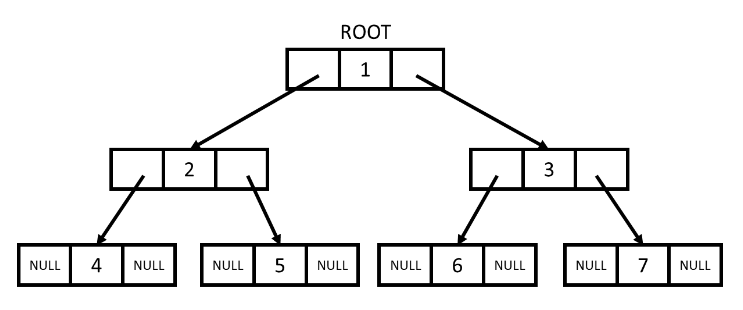
Operations on a Binary Tree

1. Insertion
2. Deletion
3. Searching
4. Traversing
5. Size of a tree
6. Height of a tree

Insertion in a Binary Tree

There is no strict rule for insertion of a node in a binary tree but other operations on binary tree are important. We will learn about other operation on a binary tree separately with proper explanation. But here we are setting up a basic method for insertion in a binary tree.

We will insert each upcoming node immediate next of root i.e., it will become the immediate child of the root node and if any child node is already present then it will be shifted to bottom and become child of that upcoming node. If root node is empty then new node will become the root node.

Insertion at left

def insert_left(root, data):
    if root:
        if root.left:
            temp = Node(data)
            temp.left = root.left
            root.left = temp
        else:
            root.left = Node(data)
    else:
        root = Node(data)

function insertLeft(root, data) {
  if (root) {
    if (root.left) {
      let temp = new Node(data);
      temp.left = root.left;
      root.left = temp;
    } else {
      root.left = new Node(data);
    }
  } else {
    root = new Node(data);
  }
}

Insertion at right

def insert_right(root, data):
    if root:
        if root.right:
            temp = Node(data)
            temp.right = root.right
            root.right = temp
        else:
            root.right = Node(data)
    else:
        root = Node(data)

function insertRight(root, data) {
  if (root) {
    if (root.right) {
      let temp = new Node(data);
      temp.right = root.right;
      root.right = temp;
    } else {
      root.right = new Node(data);
    }
  } else {
    root = new Node(data);
  }
}