Number of half nodes in a binary tree
Those nodes in the tree which have only one child are known as half nodes i.e., A node is a half node if only one child node is present among left or right child nodes. To find the number of half nodes in a binary tree, we have to traverse each node and in the tree and check if the current node is a half node or not and count them one by one.
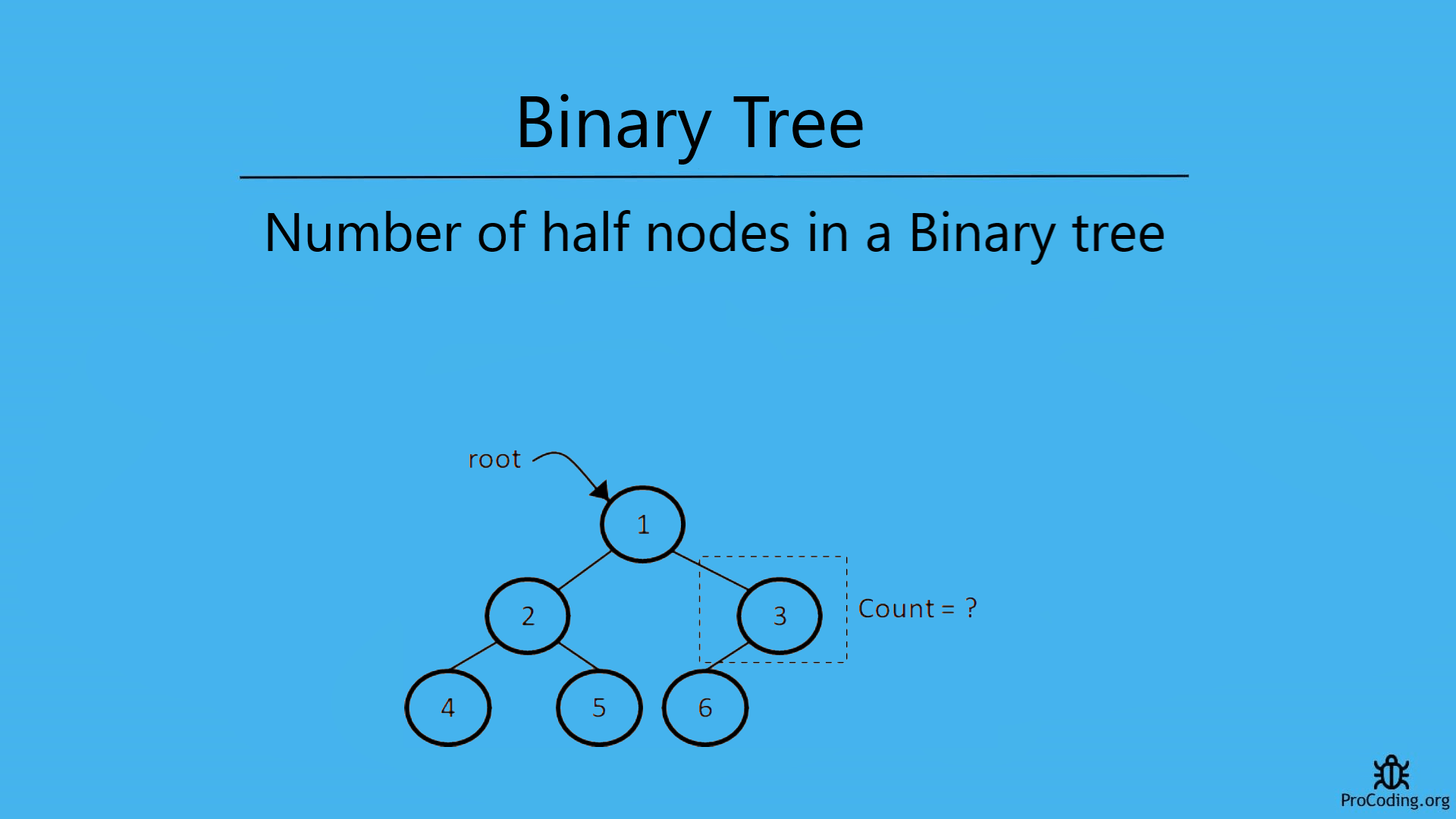
To find the number of half nodes in a binary tree, we have to traverse each node and in the tree and check if the current node is half node or not and count them one by one.
Half nodes in a binary tree
Those nodes in the tree which have only one child (either left or right child) are known as half nodes.
A node is a half node if one of the child node is null and other one has child.
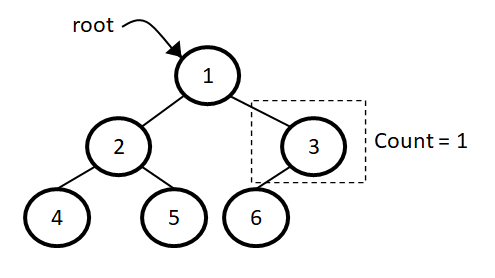
So, to count all the leaf nodes we have to traverse each node in the tree and count all those nodes which are having only one child i.e, one of the child will present and other one should be null.
Example -
Input:
1
/ \
2 3
/ /
4 6
Output: 2
We can solve this problem in two ways-
Recursive solution
For recursive solution we have to check each node one by one recursively as we have done in binary tree recursive traversal and count the nodes which are having both the children.
Algorithm
Half_Node_Count(root)
1. if root is null then
2. return 0
3. count = 0
4. if (root->left is not null and root->right is null) or
(root->left is null and root->right is not null) then
5. count = count + 1
6. left_count = Half_Node_Count(root->left)
7. right_count = Half_Node_Count(root->right)
8. count = count + left_count + right_count
9. return count
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def half_node_count(root):
if root is None:
return 0
count = 0
if (root.left and root.right is None) or (root.left is None and root.right):
count = count + 1
left_half = half_node_count(root.left)
right_half = half_node_count(root.right)
count = count + left_half + right_half
return count
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
print(half_node_count(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function halfNodeCount(root) {
if (!root) return 0;
let count = 0;
if ((root.left && !root.right) || (!root.left && root.right)) {
count++;
}
left_half = halfNodeCount(root.left);
right_half = halfNodeCount(root.right);
count = count + left_half + right_half;
return count;
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
console.log(halfNodeCount(root));
Output
1
Iterative solution
For iterative solution, we have to traverse each node in level order and count the nodes which are not having any child.
Algorithm
Half_Node_Count(root)
1. if root is null then return 0
2. queue.enqueue(root)
3. count = 0
4. while queue is not empty
5. node = queue.dequeue()
6. if (root->left is not null and root->right is null) or
(root->left is null and root->right is not null) then
7. count = count + 1
8. if node->left is not null then
9. queue.enqueue(node->left)
10. if node.right is not null then
11. queue.enqueue(node->right)
12. return count
Python
import queue
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def half_node_count(root):
if root is None:
return 0
q = queue.Queue()
q.put(root)
count = 0
while not q.empty():
node = q.get()
if (node.left and node.right is None) or (node.left is None and node.right):
count = count + 1
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
return count
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
print(half_node_count(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function halfNodeCount(root) {
if (!root) return 0;
const q = [];
q.push(root);
let count = 0;
while (q.length > 0) {
const node = q.shift();
if ((node.left && !node.right) || (!node.left && node.right)) {
count++;
}
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
}
return count;
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
console.log(halfNodeCount(root));
Output
1
Time complexity: The time complexity of both of these solution will be O(n) because we are just traversing each element of node one by one.