Maximum level sum in a binary tree
Write a program to find the maximum level sum in a binary tree even if nodes may have negative values also. To find the maximum level sum, traverse each level separately and find the sum of each level.
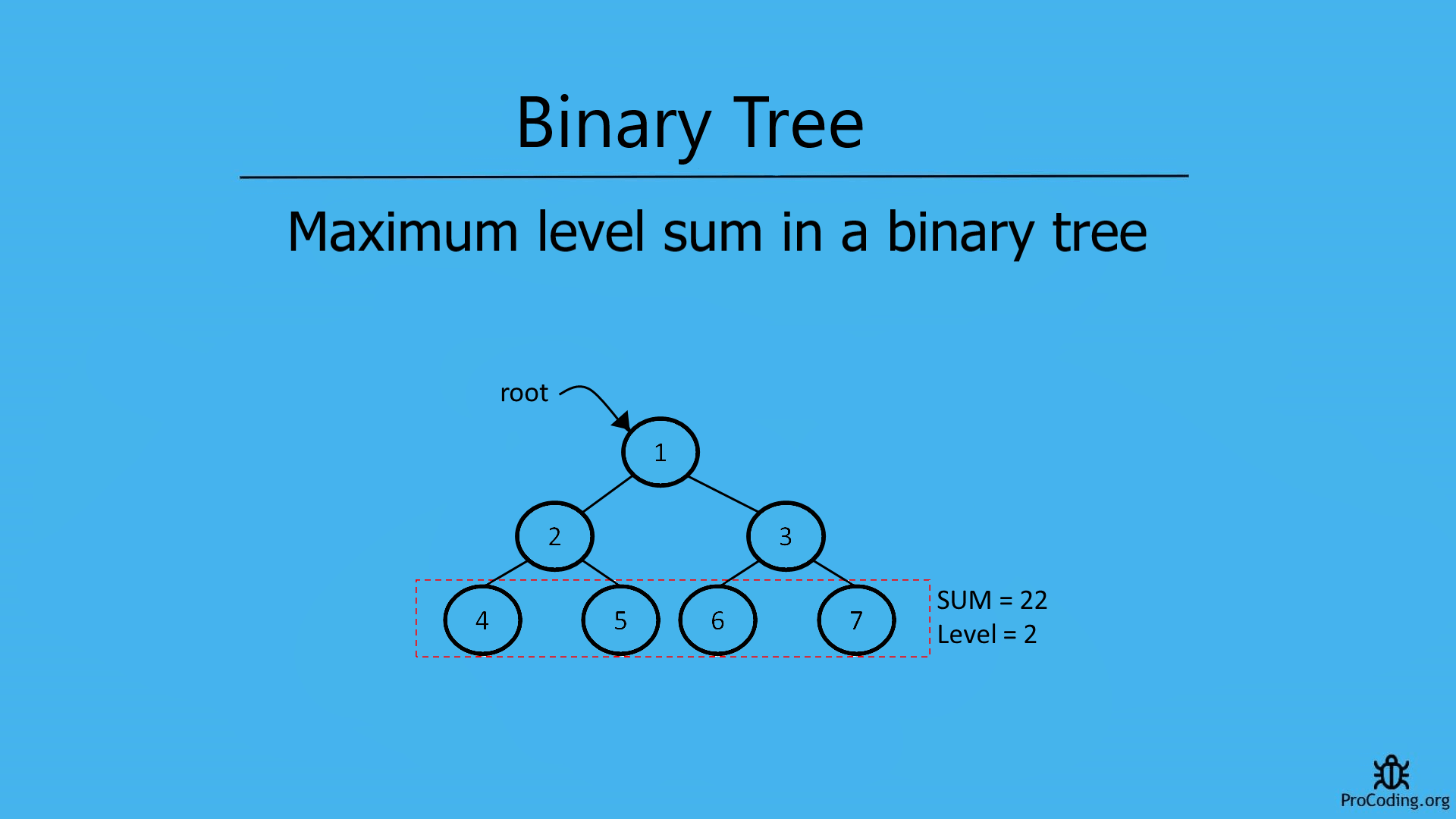
Maximum level sum in a tree
A tree has different levels, among those levels we have to identify the level having the maximum sum of nodes of elements. Nodes may also have negative values
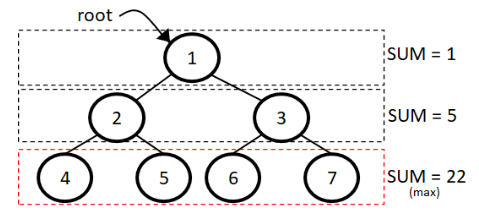
To find the maximum level sum in a binary tree we have to traverse the tree in level order and consider each level separately then compare the sum of each level.
Example -
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
Output: 2
Solution
For the solution, we have to traverse each node and this can be achieved by using level order traversal and maintain the sum of each level separately and keep comparing with the previous level of the tree having maximum sum.
Algorithm
Max_Level_Sum(root)
1. if root is not null
2. queue.enqueue(root)
3. queue.enqueue(null)
4. node = null
5. level = max_level = current_sum = max_sum = 0
6. while queue is not empty
7. node = q.dequeue()
8. if node is null then
9. if current_sum > max_sum then
10. max_sum = current_sum
11. max_level = level
12. current_sum = 0
13. if queue is not empty
14. level = level + 1
15. queue.enqueue(null)
16. else
17. current_sum = current_sum + node.data
18. if node.left is not null
19. queue.enqueue(node.left)
20. if node.right is not null
21. queue.enqueue(node.right)
22. return max_level
23. else
24. return null
Python
import queue
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def max_level_sum(root):
if root:
q = queue.Queue()
q.put(root)
q.put(None)
node = None
level = max_level = current_sum = max_sum = 0
while not q.empty():
node = q.get()
if node is None:
if current_sum > max_sum:
max_sum = current_sum
max_level = level
current_sum = 0
if not q.empty():
level += 1
q.put(None)
else:
current_sum += node.data
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
return max_level
else:
return None
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(max_level_sum(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function maxLevelSum(root) {
if (root) {
const q = [];
q.push(root);
q.push(null);
node = null;
let level, max_level, current_sum, max_sum;
level = max_level = current_sum = max_sum = 0;
while (q.length > 0) {
node = q.shift();
if (node == null) {
if (current_sum > max_sum) {
max_sum = current_sum;
max_level = level;
}
current_sum = 0;
if (q.length > 0) {
level++;
q.push(null);
}
} else {
current_sum += node.data;
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
}
}
return max_level;
} else {
return null;
}
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(maxLevelSum(root));
Output
2
Here, we have returned the level having maximum sum but if the sum value is required then return variable max_sum from the function.
Time complexity: The time complexity of this solution is O(n) because we are just traversing each element of node one by one.