Height of a binary tree
Height of a tree is the total number of nodes on the path from the root node to the deepest node in the tree. Find the height of a binary tree using the recursive and iterative solution.
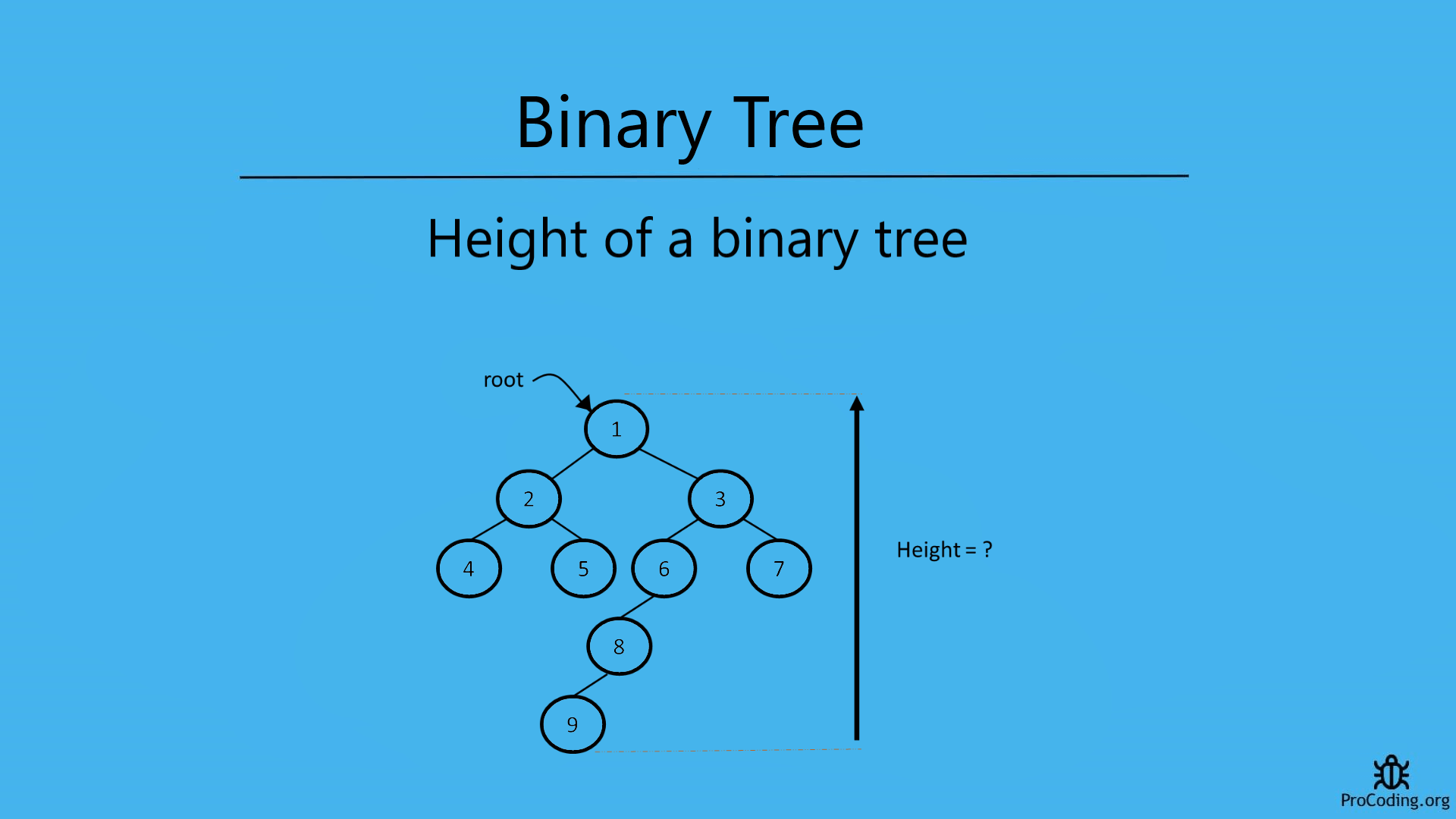
Height of a tree
It is the total number of nodes on the path from the root node to the deepest node in the tree. A tree with only a root node has a height of 1.
(Sometimes tree with one root node only considered as height 0 but here are following convention of height 1 if the tree has only onenode.)
Similary, we can calculate the height if any node in the tree i.e., total number of nodes on the path from that node to the deepest node in the tree.
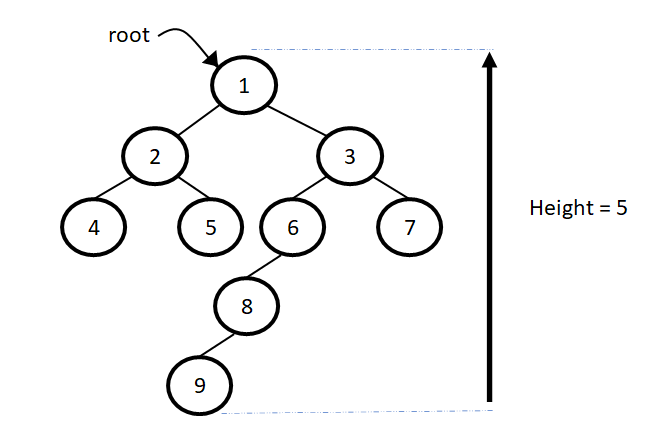
To find the height of a binary tree we have to traverse to the deepest node and then count the number of nodes in the path from root to that deepest node.
We can solve this problem in two ways-
Recursive solution
For recursive solution we have to check height of each child one by one recursively as we have done in binary tree recursive traversal. Other types of traversal can also be used.
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def height(root):
if root is None:
return 0
return max(height(root.left), height(root.right)) + 1
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(height(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function height(root) {
if (!root) return 0;
lHeight = height(root.left);
rHeight = height(root.right);
if (lHeight >= rHeight) return lHeight + 1;
else return rHeight + 1;
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(height(root));
Output
3
Iterative solution
For iterative solution, we will be following slightly similar approach as level order traversal and calculate the height.
Python
import queue
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def height(root):
if root is None:
return 0
height = 0
q = queue.Queue()
q.put(root)
while(True):
node_count = q.qsize()
if node_count == 0 :
return height
height += 1
while node_count > 0:
node = q.get()
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
node_count -= 1
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(height(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function height(root) {
if (!root) return 0;
let height = 0;
const q = [];
q.push(root);
while (true) {
nodeCount = q.length;
if (nodeCount == 0) return height;
height++;
while (nodeCount > 0) {
const node = q.shift();
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
nodeCount--;
}
}
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(height(root));
Output
3