Left rotation of an array
Given an array write a program to rotate the array of size 'n' to left/anticlockwise direction by 'k' elements and print the output. Write a program for the left rotation of an array.
We will see two different ways to solve the given problem, let's start with the simple approach, and then we will learn it with the famous Juggling algorithm.
Example -
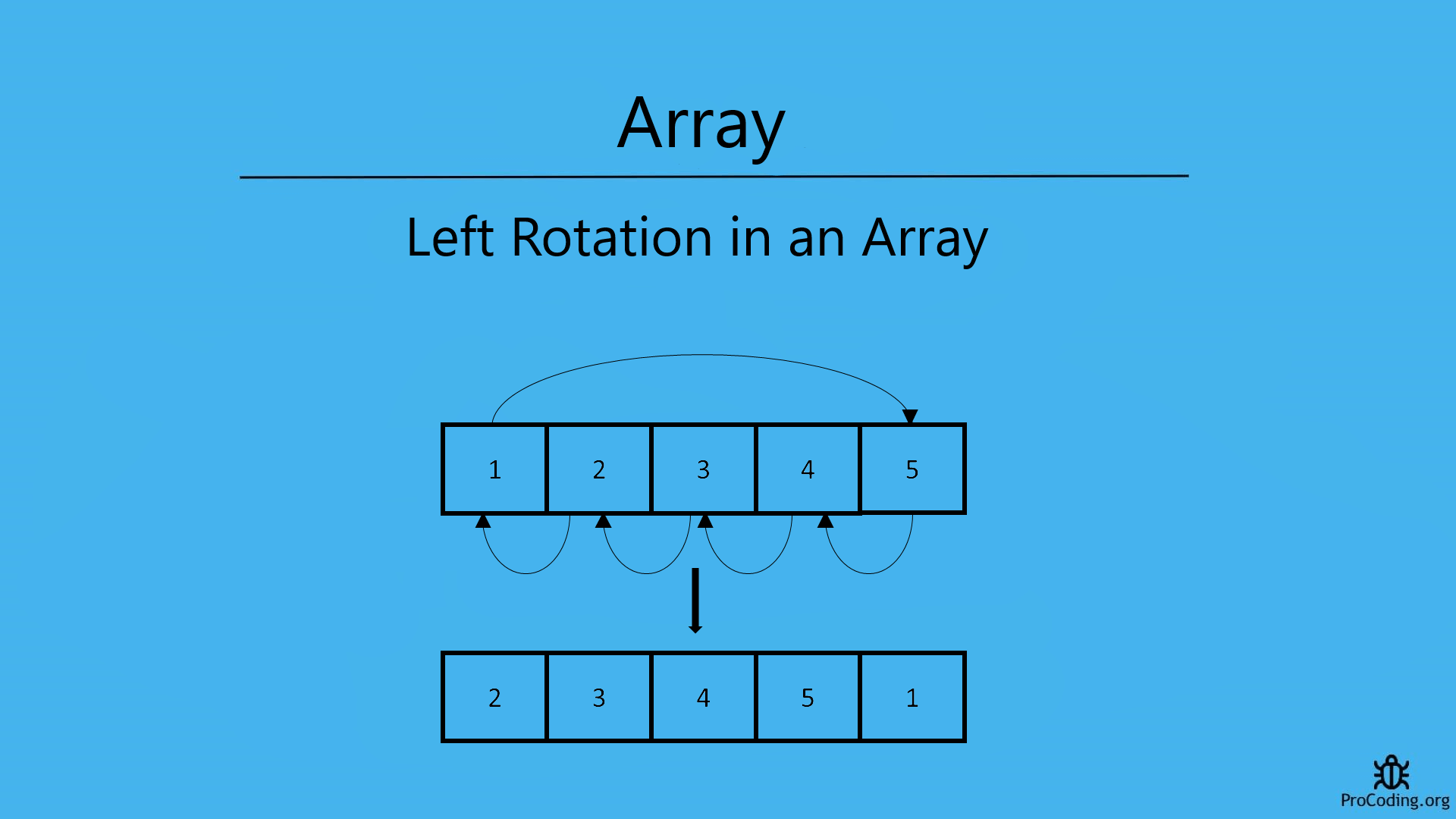
Input: arr = [ 1, 2, 3, 4, 5 ] , K = 1
Output: [ 2, 3, 4, 5, 1 ] - elements are shifted to the left by 1 position
Input: arr = [ 1, 2, 3, 4, 5, 6 ] , K = 3
Output: [ 4, 5, 6, 1, 2, 3 ] - elements are shifted to the left by 3 positions
Approach 1
In the first approach, we will be discussing an easy-to-understand method. The idea is to store the first "K" elements in a temporary array and shift the remaining elements to left and restore back the temporary array. Let us see the steps to solve the problem:
1. Store the first "K" elements in a temporary array of size "K".
2. Shift the position of the remaining elements to the left by "K" positions.
This will require a loop to store "(i+k)th" element from the starting index of the array.
3. The elements stored in the temporary array now need to be restored back to the original array.
4. Starting from "(n-k)th" index, insert the temporary array.
5. Print the array to generate the required output.
Python
def rotate_left(arr, k):
temp = []
n = len(arr)
for i in range(0, k):
temp.append(arr[i])
for i in range(k, n):
arr[i-k] = arr[i]
for i in range(n-k, n):
arr[i] = temp[i-(n-k)]
print(arr)
arr = [1, 2, 3, 4, 5]
k = 2
rotate_left(arr, k)
C++
#include <stdio.h>
#include <iostream>
using namespace std;
void rotateLeft(int arr[], int n, int k) {
int temp[k], i, j = 0;
for (i = 0; i < k; i++)
temp[i] = arr[i];
for (i = k; i < n; i++)
arr[i - k] = arr[i];
for (i = n - k; i < n; i++)
arr[i] = temp[i - (n - k)];
for (i = 0; i < n; i++) {
cout << arr[i] << " "; //print output
}
}
int main() {
int n = 5, k = 2, i;
int arr[n] = { 1, 2, 3, 4, 5 };
rotateLeft(arr, n, k);
return 0;
}
JavaScript
function rotateLeft(arr, k) {
let temp = [];
let n = arr.length;
for (let i = 0; i < k; i++) {
temp.push(arr[i]);
}
for (let i = k; i < n; i++) {
arr[i - k] = arr[i];
}
for (let i = n - k; i < n; i++) {
arr[i] = temp[i - (n - k)];
}
console.log(arr);
}
let arr = [1, 2, 3, 4, 5];
let k = 2;
rotateLeft(arr, k);
Output
3 4 5 1 2
This method will require additional space for storing "K" elements. Hence is not considered an efficient method.
Approach 2: Juggling Algorithm
In this method, we will do an in-place rotation. Hence, this will not require any additional space. We will divide the array into sets and shift every element in a set to left by “K” positions. Then move to the next step and repeat the process.
1. Divide the array into a number of sets, say "S"
• For finding "S" we need to find out the GCD of array length(N) and the number of rotations(K).
2. For every set, shift the corresponding elements by K:
Arr[j] = Arr[(j+k) % n]
3. The value of "i" will be incremented when one set is completed. This will continue for every step till "S" sets are completed.
4. Print the array to generate the required output.
Python
def gcd(n, k):
if k == 0:
return n
else:
return gcd(k, n % k)
def rotate_left(arr, k):
d = -1
n = len(arr)
for i in range(0, gcd(n, k)):
j = i
temp = arr[i]
while True:
d = (j + k) % n
if d == i:
break
arr[j] = arr[d]
j = d
arr[j] = temp
print(arr) #print output
arr = [1, 2, 3, 4, 5]
k = 2
rotate_left(arr, k)
C++
#include <stdio.h>
#include <iostream>
using namespace std;
int gcd(int n, int k) {
if (k == 0)
return n;
else
return gcd(k, n % k);
}
void rotateLeft(int arr[], int k, int n) {
int d = -1, i, temp, j;
for (i = 0; i < gcd(n, k); i++) {
j = i;
temp = arr[i];
while (true) {
d = (j + k) % n;
if (d == i) {
break;
}
arr[j] = arr[d];
j = d;
}
arr[j] = temp;
}
for (int i = 0; i < n; i++) {
cout << arr[i] << " "; //print output
}
}
int main() {
int n = 5, k = 2;
int arr[] = { 1, 2, 3, 4, 5 };
rotateLeft(arr, k, n);
return 0;
}
JavaScript
function gcd(n, k) {
if (k == 0) {
return n;
} else {
return gcd(k, n % k);
}
}
function rotateLeft(arr, k) {
let d = -1;
let n = arr.length;
for (let i = 0; i < gcd(n, k); i++) {
let j = i;
let temp = arr[i];
while (true) {
d = (j + k) % n;
if (d == i) {
break;
}
arr[j] = arr[d];
j = d;
}
arr[j] = temp;
}
console.log(arr); //print output
}
let arr = [1, 2, 3, 4, 5];
let k = 2;
rotateLeft(arr, k);
Output
3 4 5 1 2