Introduction to Binary Search Tree

A Binary Search Tree is a non-linear data structure in which all the left subtree keys should be less than the root key and all the right subtree keys should be greater than the root key. And both the left and right subtrees must also be a binary search tree.

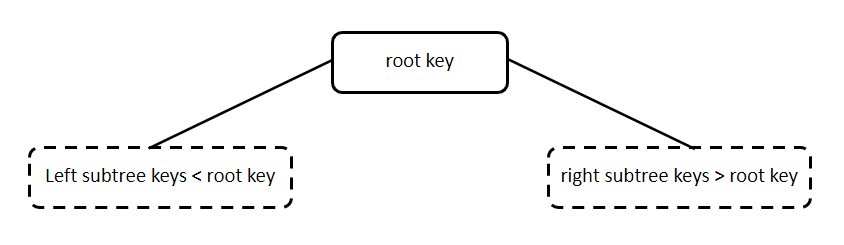
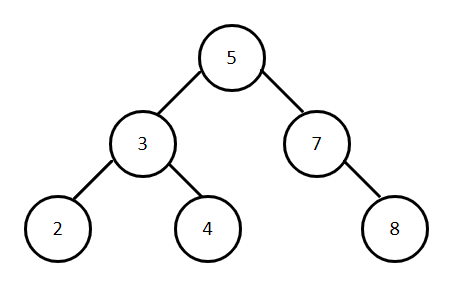
Why Binary Search Tree?

In Binary Tree we do not impose any restrictions. As a result, to search an element in the tree we have to check both left and right subtree due to this the worst-case complexity of search operation becomes O(n).

But in a Binary search tree if the tree is not skewed then the time complexity for searching an element would be O(log n).

Structure of Binary Search Tree

Structure of Binary search tree is same as Binary Tree.

class Node:
    def __init__(self, data):
        self.left = None
        self.data = data
        self.right = None

class Node {
  constructor(data) {
    this.left = null;
    this.data = data;
    this.right = null;
  }
}

Operations on Binary Search Tree

Following are the main operations on binary search tree:

• Find minimum element in binary search tree
• Find maximum element in binary search tree
• Inserting an element in binary search tree
• Deleting an element from binary search tree

Traversal (inorder, preorder, postorder and level order traversal) of binary search tree is same as the traversal of binary tree.

Apart from these operations, we will have a look into more operations on the binary search tree.

Advantages of Binary Search Tree

• Time complexity of insert, delete and search operation is reduced to O(log n).
• We have an ordering of keys stored in the tree. To get keys in increasing order, perform in-order traversal and get the keys in decreasing order perform reverse in-order traversal.

Disadvantages of Binary Search Tree

• A binary search tree is not a self-balancing tree which may result as skewed tree and then the time complexity of operations like insert, delet and the search becomes O(n).