Compare structure of two binary trees
Write a program to compare the structure of two binary trees without data and if they are identical then return true otherwise false by checking each node in the given binary trees.
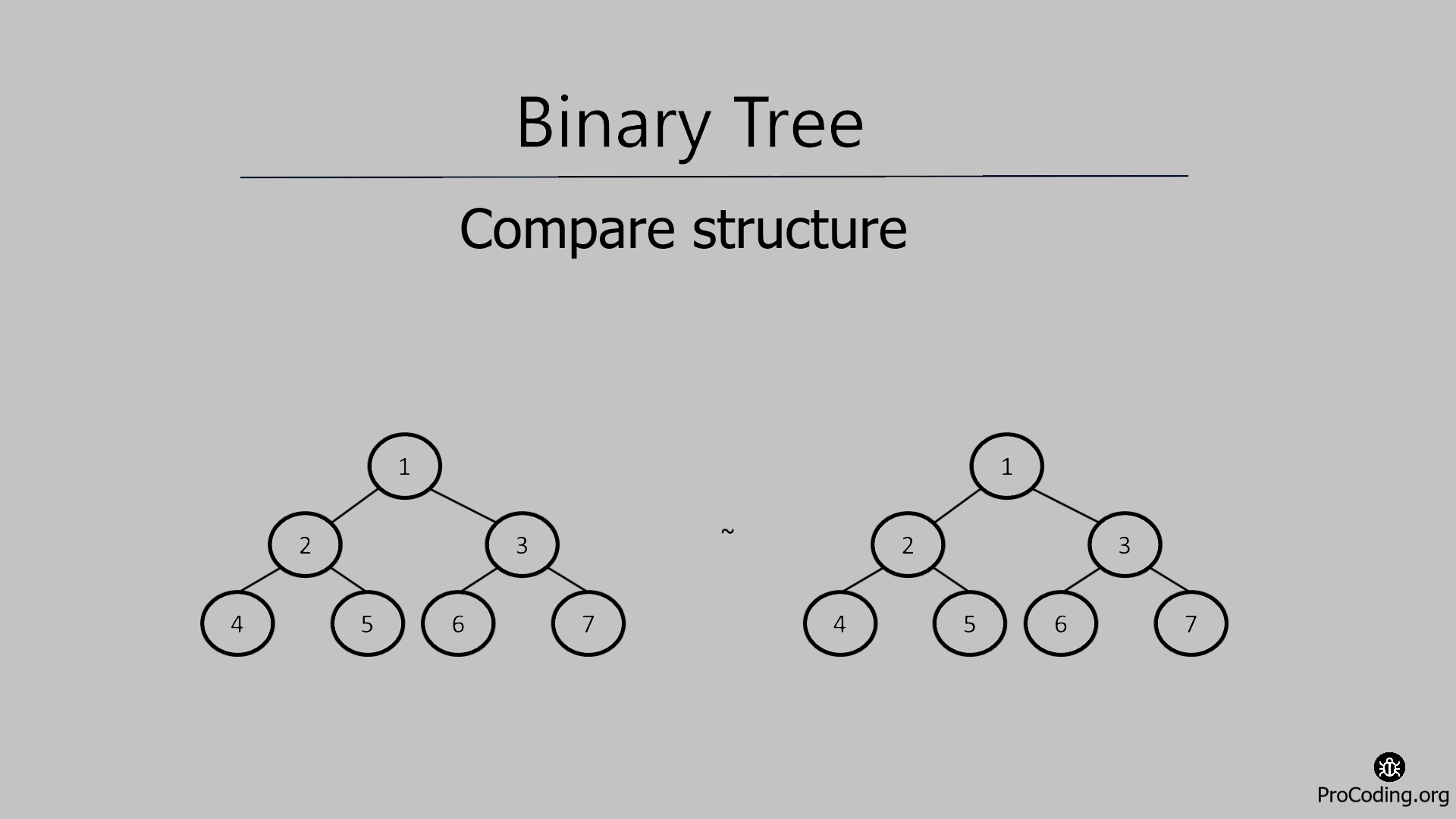
In this problem, we will try to compare the structure of two binary trees (structure only, not the data) and if the structure of both the binary trees is the same then return true otherwise false.
So we have to compare just the structure of both the given trees irrespective of the data and return the result accordingly to check if the trees are identical or not.
Example -
Input:
1 5
/ \ / \
2 3 4 6
/ / \ / / \
4 6 7 3 2 1
Output: True
Input:
1 5
/ \ / \
2 3 4 6
/ / \ / \
4 6 7 2 1
Output: False
Solution
To check if two trees are identical or having the same structure, we need to traverse both trees simultaneously, and while traversing we need to compare the presence of child/children of the trees.
Algorithm
Compare_Structure(root1, root2)
1. if root1 is null AND root2 is null then
2. return true
3. if (root1 is not null AND root2 is not null) then
4. return Compare_Structure(root1.left, root1.right) AND
return Compare_Structure(root2.left, root2.right)
5. return false
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def compare_structure(root1, root2):
if root1 is None and root2 is None:
return True
if (root1 and root2):
return compare_structure(root1.left, root1.right) and compare_structure(root2.left, root2.right)
return False
root1 = Node(1)
root1.left = Node(2)
root1.right = Node(3)
root1.left.left = Node(4)
root1.left.right = Node(5)
root1.right.left = Node(13)
root1.right.right = Node(12)
root2 = Node(1)
root2.left = Node(2)
root2.right = Node(3)
root2.left.left = Node(4)
root2.left.right = Node(5)
root2.right.left = Node(6)
root2.right.right = Node(7)
print(compare_structure(root1, root2))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function compareStructure(root1, root2) {
if (root1 == null && root2 == null) return true;
if (root1 && root2) {
return (
compareStructure(root1.left, root1.right) &&
compareStructure(root2.left, root2.right)
);
}
return false;
}
const root1 = new Node(1);
root1.left = new Node(2);
root1.right = new Node(3);
root1.left.left = new Node(4);
root1.left.right = new Node(5);
root1.right.left = new Node(6);
root1.right.right = new Node(7);
const root2 = new Node(1);
root2.left = new Node(2);
root2.right = new Node(3);
root2.left.left = new Node(4);
root2.left.right = new Node(5);
root2.right.left = new Node(6);
root2.right.right = new Node(7);
console.log(compareStructure(root1, root2));
Output
True
Time complexity: Assuming first binary tree has 'n' nodes and second binary tree has 'm' nodes then node count of the tree having less number of nodes will be considered for time complexity i.e., if n < m then time complexity will be O(n) otherwise it will be O(m).